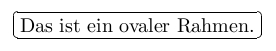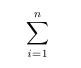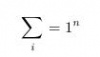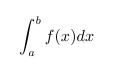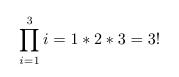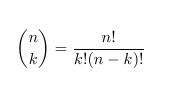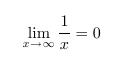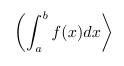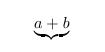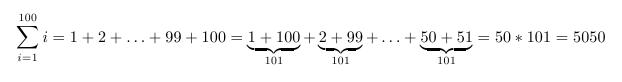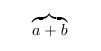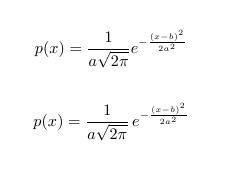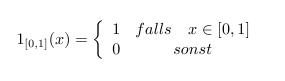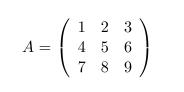LaTeX/Grundlagen 2

LaTeX   WIKI   B U C H

LaTeX: (1.) Einleitung - (2.) Schnellkurs - (3.) Teil 1 - Grundlagen - (4.) Teil 2 - Grundlagen - (5.) Fortgeschrittene - (6.) Literaturverzeichnisse - (7.) Zeichen und Symbole - (8.) LaTeX Distributionen - (9.) LaTeX Links

Grundlagen Teil 2

Die Vorführung des ersten teiles.

Weiteres Seitenlayout

Als Layout bezeichnet man eine Gesamterscheinung eines Medienproduktes.

Titel

Zum definieren eines Titels verwenden wir:

\begin{document}
 \begin{titlepage} LaTeX \end{titlepage}
\end{document}

Dies würde eine zusätzliche Seite in unserem Dokument erstellen auf dessen der angegebene Titel in diesem falle LaTeX zu sehen ist.

Titel, Autor, Datum

Eine weitere bequeme Möglichkeit für

• Titel
• Autor
• Datum

\documentclass[a4paper,10pt]{article}

\usepackage[ngerman]{babel}

\title{LaTeX \\ Artikel} 
\author{Linux-Club.de}
\date{12.11.2005}


\begin{document}
 \maketitle
  Hier wäre nun der eigentliche Text unseres Dokumentes zu finden...
\end{document}

Die Titelseite wird an der Stelle erstellt an welcher der Befehl \maketitle im Dokument steht. Aussehen könnte dies dann so wie im Beispiel:

Beispiel: Titel, Author, Datum unter LaTeX.

Neue Seite

Eine neue Seite kann ganz simpel mit dem Befehl:

\newpage

erstellt werden.

Seitennummerierung

Bei der Paginierung oder Seitennummerierung besteht die Möglichkeit der Abschaltung von Seitenzahlen, was aber nicht immer zu empfehlen ist. Besonders bei der Verwendung eines Inhaltverzeichnisses. Hier wird gezeigt wie es geht:

\pagenumbering{empty}

Würde die Seitenzahlen deaktivieren und muss in die Präambel geschrieben werden.

Römische Seitenzahlen

Anstelle unserer üblichen Seitenzahlen, können auch Römische Zahlen verwendet werden, dazu folgendes in die Präambel schreiben.

\pagenumbering{roman}

roman

Seitenzahl in Buchstaben

Wem es gefällt oder wer es benötigt kann anstelle von Seitenzahlen auch Buchstaben verwenden. Dazu diesen Eintrag in die Präambel mit aufnehmen.

\pagenumbering{Alph}

alph

Auflistungen

Bei einer Auflistung haben wir verschiedene Möglichkeiten der Darstellung.

Punkt Auflistung

Der entscheidende Punkt ist hier itemize.

\begin{document}
 \begin{itemize}
  \item Zucker
  \item Salz
  \item Mehl
 \end{itemize}
\end{document}

Beispiel einer Punkt Auflistung unter LaTeX.

Zahlen Auflistung

Der wichtige Punkt ist hier enumerate, ansonsten bleibt alles beim alten.

\begin{document}
 \begin{enumerate}
  \item Zucker
  \item Salz
  \item Mehl
 \end{enumerate}
\end{document}

Beispiel einer Zahlen Auflistung unter LaTeX.

Schlagwort Auflistung

Bei description kann das Schlagwort selbst bestimmt werden, in diesem Falle ( Punkt 1 bis Punkt 3 ).

\begin{document}
 \begin{description}
  \item [Punkt 1] Zucker
  \item [Punkt 2] Salz
  \item [Punkt 3] Mehl
 \end{description}
\end{document}

Beispiel einer Schlagwort Auflistung unter LaTeX.

Fußnoten

Es ist recht simpel mit dem Befehl \footnote eine Fußnote einzufügen. Hierbei sollte allerdings beachtet werden, das bei:

• Report
• Book

die Fußnoten nicht komplett durchnummeriert werden, sondern Kapitelweise.

\begin{document}
 Hier schreibe ich jetzt mal einen kleinen Text \footnote{Damit ist dieser Text gemeint} 
 bei dem ich eine Randnotiz einfügen möchte. Wie man nun sehen kann wurde 
 die Fußnote ganz unten auf dieser Seite eingefügt.
\end{document}

Beispiel einer Fußnote unter LaTeX.

Randnotiz

Sollte mal ein Text verfasst werden bei dem es nötig sein sollte eine Randnotizen hinzuzufügen so kann dies mit \marginpar bewerkstelligt werden.

\begin{document}
 \noindent
  Hier schreibe ich jetzt mal einen kleinen Text \marginpar{Notiz} bei dem ich eine 
  Randnotiz einfügen möchte. Wie man nun sehen kann wurde das Wort \textbf{Notiz} 
  als Randnotiz am Rechten Rand eingefügt.
\end{document}

Beispiel einer Randnotiz unter LaTeX.

Zitate

Wer einen Text mit einem Zitat verfasst, kein Problem. Auf beiden Seiten eingerückte Zitate können ganz einfach geschrieben werden.

Beispiel:

\begin{document}
 Ein Zitat bedeutet, das ich einen Text oder eine entsprechende Textstelle von irgend wo anders übernehme.

  \begin{quote}
   Dies ist nun das Zitat.
  \end{quote}

 Ein Zitat wäre also ein expliziter Hinweis auf einen anderen Autoren. Man sollte aus Anstandsgrüden bei einem Zitat die Quelle oder ein  Literaturnachweis angeben.
\end{document}

Beispiel mit einem Zitat unter LaTeX.

Literaturverzeichnis

Das einfügen von Literaturverzeichnissen ist ein bisschen aufwändiger, aber deshalb nicht schwerer. Wir müssen lediglich erst eine Umgebung für das Literaturverzeichnis schaffen.

\begin{document}
 \begin{thebibliography}{------}

 \end{thebibliography}
\end{document}

Mit den 6 Minuszeichen in den geschweiften Klammer, wird die spätere Breite des labels bestimmt, was natürlich entsprechend angepasst werden kann. Im Gesamten kann dies dann so aussehen:

\begin{document}
 \begin{thebibliography}{------}
  \bibitem[Tux]{Tux}
   Linus Benedict Torvalds.
   {\em Software is like sex. Its better when its free.}
   17. September 1991
 \end{thebibliography}
\end{document}

Beispiel eines Literaturverzeichnis unter LaTeX.

Abstände

Man kann unter LaTeX bei Texten oder auch Bildern bestimmte Abstände einfügen. Hier hat man dann die Wahl zwischen:

• mm
• cm
• pt

Abstand horizontal

Wir machen uns hierzu \hspace zunutze:

\begin{document}
 Das ist mein Text in dem jetzt \hspace{3 cm} ein drei cm Abstand ist.
\end{document}

Horizontaler Abstand unter LaTeX.

Die Maßeinheit ist hier cm.

Abstand vertikal

Beim vertikalen einfügen eines Abstandes verwenden wir den Befehl: \vspace.

\begin{document}
 Das ist mein Text in dem jetzt 

 \vspace{1 cm} 

 ein ein cm Abstand ist.
\end{document}

Vertikaler Abstand unter LaTeX.

Die Maßeinheit ist hier cm.

Mehrspaltiger Text

Für einen Mehrspaltigen Text müssen wir zuerst ein weiteres Paket mit in die Präambel aufnehmen um dieses zu laden, der entsprechende Befehl heisst:

\usepackage{multicol}

Das Kommande zur Verwendung ist dann so aufgebaut:

\begin{multicols}{spaltenzahl}[titel]
 \end{multicols}

Zwei Spalten

\begin{document}

 \begin{multicols}{2}[Das ist der Titel]
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
 \end{multicols}

\end{document}

Beispiel eines zweispaltigen textes unter LaTeX

Drei Spalten

\begin{document}

 \begin{multicols}{3}[Das ist der Titel]
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
  Hier ist ein Mehrspaltiger Text zu sehen.
 \end{multicols}

\end{document}

Beispiel eines dreispaltigen textes unter LaTeX

Weiteres

Weitere Möglichkeiten die wir haben sind zum Beispiel die Verwendung eines Striches zwischen den Spalten, genauso kann der Abstand zwischen diesen Spalten bestimmt werden oder die dicke des Trennstriches zwischen den Spalten.

Spaltenabstand

Hier wird zuerst angegeben in welchem Abstand wir unsere Spalten möchten.

\setlength{\columnsep}{1cm}

Strichdicke

Hier wird unsere Strichdicke in der Masseinheit pt = Punkt Grösse angegeben.

\setlength{\columnseprule}{0.5pt}

Beispiel Zweispaltig

\begin{document}

 \setlength{\columnsep}{1cm}
  \setlength{\columnseprule}{0.5pt}
   \begin{multicols}{2}[Das ist der Titel]
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
   \end{multicols}

\end{document}

Beispiel eines zweispaltigen textes unter LaTeX

Beispiel Vierspaltig

Es geht natürlich genauso bei noch mehr Spalten:

\begin{document}

 \setlength{\columnsep}{1cm}
  \setlength{\columnseprule}{0.5pt}
   \begin{multicols}{4}[Das ist der Titel]
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
    Hier ist ein Mehrspaltiger Text zu sehen.
   \end{multicols}

\end{document}

Beispiel eines vierspaltigen textes unter LaTeX

Textrahmen

Ab und an wird auch mal ein Rahmen um einen Text benötig, ich möchte hier kurz zeigen wie das genau funktioniert.

frame

\begin{document}
 \frame{Das ist ein Rahmen.}
\end{document}

Beispiel eines Textrahmen mit frame unter LaTeX

fbox

\begin{document}
 \fbox{Das ist ein Rahmen.}
\end{document}

Beispiel eines Textrahmen mit fbox unter LaTeX

framebox

\begin{document}
 \framebox[5,0cm]{Das ist ein Rahmen.}
\end{document}

Beispiel eines Textrahmen mit framebox unter LaTeX

Spetzielle Rahmen

Es gibt noch weitere spetzielle Textrahmen für die man allerdings ein zusätzliches Paket benötigt. Um dieses Zusätzliche Paket verwenden zu können, schreiben wir wieder einen kleinen Eintrag in unsere Präambel:

\usepackage{fancybox}

OvalBox

\begin{document}
 \ovalbox{Das ist ein ovaler Rahmen.}
\end{document}

Beispiel eines Textrahmen mit ovalbox unter LaTeX

ShadowBox

\begin{document}
 \shadowbox{Das ist ein Rahmen mit Schatten.}
\end{document}

Beispiel eines Textrahmen mit shadowbox unter LaTeX

Grafik einbinden

Wer einmal eine Grafikdatei in sein Dokument einbinden muss ist hier richtig. Ich beschreibe ein paar unterschiedliche Wege dies zu tun, da es veraltete wie auch neuere Möglichkeiten gibt.

epsfig

Die bereits ältere Methode welche aber dennoch funktioniert wäre epsfig welches ich als erstes vorstellen möchte. Zuerst muss in die Präambel der entsprechende Eintrag hinzugefügt werden damit das Paket geladen wird.

\usepackage{epsfig}

Nachdem der Eintrag in die Präambel hinzugefügt wurde, möchte ich darauf hinweissen das bei der Verwendung von epsfig nur Dateien im Encapsulated PostScript Format verwendet werden können. Dies soll heissen, das Bilder welche sich in einem anderen Dateiformat befinden bei einer gewünschten Verwendung erst umgewandelt werden müssen. Das Umwandeln aus einem *.jpeg, *.bmp, *.gif oder *.png geht recht einfach und sollte jede einfach Bildbearbeitungssoftware beherschen. Ich selbst empfehle für solche Dinge das Bildmanipulationsprogramm GIMP welches für die meisten Plattformen zur verfügung steht. Hat meine eine Grafik im *.eps Format forliegen, so kann diese mit dem Befehl \epsfig{file=< dateiname >.eps} eingebunden werden.

\epsfig{file=tux.eps}

Hierbei wird dann die Datei tux.eps in das Dokument eingebunden was dann so aussehen kann:

\documentclass[a4paper,10pt]{article}

\usepackage[ngerman]{babel}
\usepackage{epsfig}

\begin{document}

 \epsfig{file=tux.eps}

\end{document}

Beispiel mit epsfig und einer *.eps Datei unter LaTeX.

Anstelle von *.eps Grafiken, können mit Hilfe von epsfig auch PS - PostScript Dateien eingefügt werden. Hierbei wird vollgender Befehl verwendet:

 \epsfig{figure=beispiel.ps}

Hier würde die Datei beispiel.ps als Grafik in das Dokument eingebunden werden.

\documentclass[a4paper,10pt]{article}

\usepackage[ngerman]{babel}
\usepackage{epsfig}

\begin{document}

 \epsfig{figure=beispiel.ps}

\end{document}

Beispiel mit epsfig und einer als Grafik eingebundenen PostScript Datei unter LaTeX.

Bild Titel

Einer eingebundenen Grafik kann auch ein Titel mitgegeben werden was so aussehen würde. Zuerst sollte hierfür eine passende umgebung geschaffen werden.

\begin{document}

 \begin{figure}
 \end{figure}

\end{document}

Anschliessend kann man ein Bild mit Titel in das Dokument einfügen:

\begin{document}

 \begin{figure}

  \epsfig{file=tux.eps}
   \caption{Das ist Tux der Pinguin}

 \end{figure}

\end{document}

Beispiel mit epsfig und einem Bild mit Titel unter LaTeX.

Grafiken Platzieren

Im Dokument eingefügte Grafiken können an verschiedenen Stellen platziert werden, hierfür werden drei Buchstaben verwendet:

• h
• t
• b

Mit (h) wird versucht die eingefügte Grafik an der Stelle im Dokument zu platzieren an dieser auch der entsprechende Befehl in der Quelldatei steht. Sollte der Befehl auf der 2ten von 3 Seiten sein, so wird versucht die Grafik auf der zweiten Seite einzufügen. Der Buchstabe (t) versucht die Grafik an den Anfang des entsprechenden dokumentes zu platzieren, das bedeutet das versucht wird die Grafik auf der ersten Seite darzustellen. Und zuguterletzt wird durch (b) versucht die Grafik an das Ende des Dokumentes zu setzen.

Hier zwei Beispiele dazu:

\begin{document}
Das ist ein Text...

 \begin{figure}[h]

  \epsfig{file=tux.eps}

 \end{figure}
 ...und hier ein weiterer Text

\end{document}

Beispiel mit epsfig und (h) unter LaTeX.

\begin{document}
Das ist ein Text...

 \begin{figure}[t]

  \epsfig{file=tux.eps}

 \end{figure}

 ...und hier ein weiterer Text
\end{document}

Beispiel mit epsfig und (t) unter LaTeX.

Bei b würde eine neue weitere letzte Seite erzeugt an diese die Grafik gestellt wird.

\begin{document}
Das ist ein Text...

 \begin{figure}[b]

  \epsfig{file=tux.eps}

 \end{figure}

 ...und hier ein weiterer Text
\end{document}

Beispiel mit epsfig und (b) auf der letzten Seite im Dokument.

Umranden

Umranden können wir mit \fbox{} so auch bei eingefügten Grafiken, hier ein Beispiel:

\begin{document}
Das ist ein Text...

 \begin{figure}[h]

  \fbox{
   
   \epsfig{file=tux.eps}

  }

 \end{figure}

 ...und hier ein weiterer Text
\end{document}

Beispiel mit epsfig und fbox unter LaTeX.

Der Inhalt der geschweiften {..}Klammern beim Befehl fbox wird umrandet.

graphicx

Hier möchte ich nun die zweite und damit neuer Möglichkeit zeigen um Grafik in ein Dokument einzufügen. Als erstes müssen wir wieder ein Paket laden und hier den entsprechenden Befehl in die Präambel mit aufnehmen.

\usepackage{graphicx}

Mit dem Paket graphicx ist es uns möglich, weitere Dateiformate in unser Dokument einzufügen. Zu diesen geören zum Beispiel *.jpeg, *.png oder auch *.bmp. Der kleine aber feine Unterschied im Vergleich zu dem *.eps Format ist der, das die Bildgrösse expliziet mit angegeben werden muss. Bei einer *.eps Datei werden diese Informationen der Grafikdatei entnommen. Funktionieren tut das angeben der Grösse vollgendermassen:

[bb=0 0 165 198]

Wie im Beispiel zu sehen sind hier die Zahlen 230 und 276 vorhanden welche nichts anderes bedeuten als 230x276 PostScript-Punkte. Diese sogenannten PostScript-Punkte sind bitte nicht zu verwechseln mit den sogenannten Pixeln. Die beiden Grössen, PostScript-Punkte und Pixel lassen sich aber ineinander umrechnen. Hierbei entspricht 1PostScript-Punkte ungefähr 1,39 Pixel. Die Pixelgrösse mal 0,72 ergiebt dann die PS-Points. Die beiden Nullen müssen unbedingt angegeben werden. Hier noch einmal gerechnet anhand eines beispieles:

Unser Bild hat 230 x 276 Pixel, also rechnen wir:

230 x 0.72 = 165

276 x 0.72 = 198

Die 165x198 PostScript-Punkte sind dann wie oben im Beispiel zu schreiben.

Der gesammte Eintrag für ein Bild würde dann so aussehen:

\begin{document}
 \begin{figure}

  \includegraphics[bb=0 0 165 198]{tux.png}

 \end{figure}
\end{document}

Hier würde dann die Grafikdatei tux.png in das Dokument eingefügt werden.

Beispiel mit graphics und einer *.png Grafikdatei unter LaTeX.

Bild Titel

Ein Titel für das Bild wird auf die gleiche Art und Weisse mit angegeben wie bei der Verwendung von epsfig.

\begin{document}
 \begin{figure}

  \includegraphics[bb=0 0 165 198]{tux.png}
   \caption{Das ist Tux der Pinguin}

 \end{figure}
\end{document}

Beispiel mit graphics und einem Bildtitel unter LaTeX.

Grafiken Platzieren

Auch hier wird genau so vorgegangen wie bereits im epsfig Teil weiter oben erwähnt. Durch genau das selbe Vorgehen, zeige ich hier nur ein Beispiel, und verweisse auf Punkt 1.3.1.2

\begin{document}
 \begin{figure}[h]

  \includegraphics[bb=0 0 165 198]{tux.png}
   \caption{Das ist Tux der Pinguin}

 \end{figure}
\end{document}

Beispiel mit graphics und der Prosition (h) unter LaTeX.

Umranden

Auch beim umranden der Grafik verwenden wir das selbe vorgehen wie unter epsfig Punkt 1.3.1.3

\begin{document}

 Ich bin der Tux...

  \begin{figure}[h]

   \fbox{
    \includegraphics[bb=0 0 165 198]{tux.png}
   }

  \end{figure}

 ...der Linux Tux aus Tuxhausen.

\end{document}

Beispiel mit graphics und Rahmen um die eingebundene Grafik unter LaTeX.

Tabellen

Ab und an ist es nötig in dem Dokument welches man gerade verfasst eine Tabelle zur besseren darstellung zu verwenden. Wie man genau eine Tabelle unter LaTeX in einem Dokument erstellt möchte ich hier zeigen.

Tabellenumgebung

Zuerst benötigen wir eine passende Umgebung für diese Tabelle, welche wir so erzeugen.

\begin{document}

 \begin{tabular}{|l|c|r|}
 \end{tabular}

\end{document}

Tabelleninhalt

Für jede Spalte benötigen wir einen Buchstaben, welche dann der Ausrichtung dienen. Ich habe in diesem beispiel drei Buchstaben angegeben für eine Tabelle mit drei Spalten. Getrennt werden diese drei Buchstaben durch den wagerechten Strich | welche die Begrenzung d.h. die Spaltenlinien darstellt. Die Bedeutung der drei Buchstaben ist vollgende. Durch l was ein kleinen L ist wird der Inhalt linksbündig dargestellt. Durch das kleine c wird dieser genau in der Mitte, also Zentriert dargestellt. Das kleine c steht also für das Wort Center. Zuguterletzt wie soll es auch anderst sein, haben wir noch das kleine r als Buchstaben welches für einen rechtsbündigen Inhalt steht.

• l - left
• c - center
• r - right

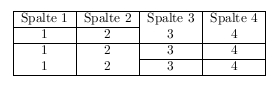
Hier nun der Tabelleninhalt:

\hline
Spalte 1 & Spalte 2 & Spalte 3\\ \hline
1 & 2 & 3\\ \hline

Wie in diesem Beispiel zu sehen, haben wir den Befehl \hline verwendet der eine horizontallinie ausgiebt. Spalte 1,Spalte 2 und Spalte 3 geben den Inhalt der drei Spalten aus. Genau soll das heissen, das ihr die drei Wörter Spalte... ersetzten könnt durch irgend etwas anderes was später in der Tabelle stehen soll. Getrennt werden die einzelnen Spalten der Tabelle duch das UND Zeichen &. Die Zahlen 1 , 2 und 3 sind die Inhalte der zweiten Tabellenzeile und werden wie in der ersten Zeile durch das UND Zeichen & getrennt. Der Befehl \\ erzwingt einen Zeilenumbruch wie wir ihn schon zum Anfang des Buches kennengelernt haben.

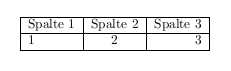
Tabellenbeispiel

Als fertiger Quelltext müsste dies dann so aussehen:

\begin{document}

 \begin{tabular}{|l|c|r|}

  \hline
   Spalte 1 & Spalte 2 & Spalte 3\\ \hline
   1 & 2 & 3\\ \hline 

 \end{tabular}

\end{document}

Beispiel einer dreispaltigen Tabelle unter LaTeX.

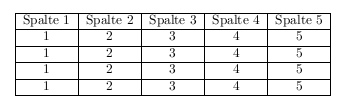
Grössere Tabelle

Hier ein weiteres Beispiel einer etwas grösseren Tabelle mit 5 Spalten und 5 Zeilen, aber genau der gleiche Prinzip bzw. das gleiche vorgehen. Die kleine Besonderheit wäre hier das im Vergleich zur ersten Tabelle der Inhalt aller Spalten durch c Zentreirt wurde.

\begin{document}
 \begin{tabular}{|c|c|c|c|c|}
  \hline
   Spalte 1 & Spalte 2 & Spalte 3 & Spalte 4 & Spalte 5\\ \hline
   1 & 2 & 3 & 4 & 5\\ \hline
   1 & 2 & 3 & 4 & 5\\ \hline 
   1 & 2 & 3 & 4 & 5\\ \hline 
   1 & 2 & 3 & 4 & 5\\ \hline 
 \end{tabular}
\end{document}

Beispiel einer 5 Spalten u. Zeilen Tabelle unter LaTeX.

Zusammenfügen von Zeilen

Wer in einer Tabelle div. Zeilen zusammen fügen muss, kann dies mit Hilfe von cline erledigen.

\begin{document}

 \begin{tabular}{|c|c|c|c|}

  \hline

   Spalte 1 & Spalte 2 & Spalte 3 & Spalte 4 \\ 

   \cline{1-2} 1 & 2 & 3 & 4 \\ \hline
               1 & 2 & 3 & 4 \\  
   \cline{3-4} 1 & 2 & 3 & 4 \\ \hline 

 \end{tabular}

\end{document}

Wir geben in unserem Beispiel mit cline in den geschweiften Klammern an das wir die Zeilen 1 und Zeile 2 der Spalten 1 und Spalte 2 weiterhin mit einer Horizontallinie trennen, da der Befehl für die Horizontallinie in diesem Quellcode nicht mehr vorhanden ist um zwei Zeilen zusammen zu fügen.

Schaut euch diesen Quellcode mit dem einer normalen Tabele weiter oben etwas genauer an und ihr werdet feststellen, das der Befehl \hline an zwei Stellen nicht mehr vorhanden ist.

Genau das gleiche gilbt auch fuer die Zeile 3 und Zeile 4 sowie fuer die Spalten 3 und Spalte 4.

Beispiel einer Tabelle unter LaTeX.

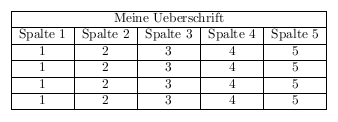
Tabellen Überschrift

Wir haben nun vor einer Tabelle noch eine kleine mehrspaltige Überschrift zu geben. Dazu verwenden wir den Befehl \multicolumn. Wir geben in den ersten geschweiften Klammern die Spaltenanzahl ein, über die sich unsere Überschrift erstrecken soll. In den zweiten geschweiften Klammern geben wir unsere Ausrichtung an wie wir sie schon weiter oeben kennengelernt haben l,c,r. Und in den dritten geschweiften Klammern unseren Überschriftstext.

\multicolumn{Spaltenanzahl}{Ausrichtung}{Der Text}

In einer Tabelle kann dies dann zum Beispiel so aussehen:

\begin{document}
 \begin{tabular}{|c|c|c|c|c|}
  \hline
   \multicolumn{5}{|c|}{Meine Ueberschrift}\\ \hline
    Spalte 1 & Spalte 2 & Spalte 3 & Spalte 4 & Spalte 5\\ \hline
    1 & 2 & 3 & 4 & 5\\ \hline
    1 & 2 & 3 & 4 & 5\\ \hline 
    1 & 2 & 3 & 4 & 5\\ \hline 
    1 & 2 & 3 & 4 & 5\\ \hline 
 \end{tabular}
\end{document}

Beispiel einer Tabellenüberschrift unter LaTeX.

Linien

Um unter LaTeX Linien zu erstellen, nutzen wir den Befehl line mit den Angaben für die Horizontale, Vertikale Prosition und der Angabe für die Länge unserer Linie.

Die Syntax:

\line(h,v){l}

Das (h) steht für Horizontale das (v) für die Vertikale und das (l) für die Länge der Linie. Die Zahlenwerte reichen hierbei von -6 über 0 bis zu +6.

Horizontal

\line(1,0){50}

Beispiel einer Linie unter LaTeX.

Vertikal

\line(0,1){50}

Beispiel einer Linie unter LaTeX.

Pfeillinien

Anstelle von normalen Linien, können auch Pfeillinien gezeichnet werden, hierzu den Befehl \vector einsetzen.

Horizontal Pfeil

\begin{document}
 \vector(1,0){20}
\end{document}

Beispiel einer Pfeillinie unter LaTeX.

Vertikal Pfeil

\begin{document}
 \vector(0,1){20}
\end{document}

Beispiel einer Pfeillinie unter LaTeX.

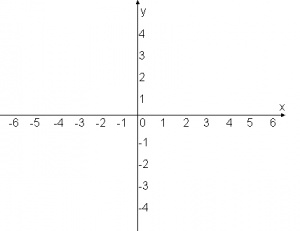
Kordinatensystem

Für die Prositionierung von Grafiken wird unter LaTeX ein Kordinatensystem verwendet, welches eine Wagerechte X-Achse und eine Senkrechte Y-Achse verwendet. Der Schnittpunkt der beiden Achsen ist hier bei der Bezugspunkt (0,0). Mit dieser Möglichkeit, können alle Grafiken an eine bestimmte Prosition gebracht werden.

Beispiel Kordinatensystem für x & y Achse im +/- Bereich.

Picture Umgebung

Die Picture Umgebung definiert den Bereich in welchem die Liniengraphik verwendet werden kann.

\begin{picture}(Breite,Höhe)(X,Y) 

\end{picture}

Die Breite und auch die Höhe im Befehl, geben die Breite und Höhe des Bildes an. x und y verschieben das Bild in horizontaler und vertikaler Richtung. Zudem sind die Werte (X und Y) optional.

Damit man sich so eine Umgebung besser vorstellen kann, empfehle ich hier am Anfang als kleine Hilfe einfach einen Rahmen herrum zeichenen zu lassen. Hier mal schnell ein kleines Beispiel mit einem Rahmen der durch \fbox erzeugt wird.

\begin{document}

 \fbox{

  \begin{picture}(180,100)
  \end{picture}

 }
\end{document}

Wie schon im Quelltext zu sehen, erstelle ich hier eine Umgebung welche eine Breitenangabe von 180 und eine Höhe von 100 hat. Nach Adam Riese und Eva Stein ist dies dann ein Rechteck welches breiter als höher ist.

Umrisse einer Picture Umgebung unter LaTeX.

In diese sogenatennte Picture Umgebung kann nun etwas gezeichnet werden, Linien, Pfeile oder auch Kreise sind möglich. Der Phantasie sind hier keine Grenzen gesetzt, einfach mal ein bisschen herrum spielen.

Objekt Positionieren

Um nun ein Objekt in einer Picture Umgebung genau positionieren zu können, verwenden wir den Befehl \put.

\put(X, Y){Objekt}

Mit dem Zahlenpaar für X und Y wird das Objekt an genau dieser Stelle in der Picture Umgebung dargestellt.

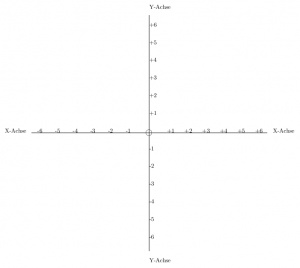
Beispiel Zeichnung

Wer nun das Kordinatensystem verstanden hat, weiss was eine Picture Umgebung ist und wie man Pbjektprositionen bestimmt, kann sich dieses Beispiel einmal ansehen. Alleine durch die hier in diesem Buch vorgestellten Befehle, ist man bereits in der Lage vollgendes Kordinatensystembeispielbild zu erstellen.

Hier mein Quelltext zum Bild:

\begin{document}
 \begin{picture}(400,400)
  \put(0.0,200.0){\line(6,0){400.0}} 
  \put(410.200,200.200){X-Achse} 
  \put(230.200,200.200){+1}
  \put(260.200,200.200){+2}
  \put(290.200,200.200){+3}
  \put(320.200,200.200){+4}
  \put(350.200,200.200){+5}
  \put(380.200,200.200){+6}
  \put(-45.200,200.200){X-Achse} 
  \put(160.200,200.200){-1}
  \put(130.200,200.200){-2}
  \put(100.200,200.200){-3}
  \put(70.200,200.200){-4}
  \put(40.200,200.200){-5}
  \put(10.200,200.200){-6}
  \put(200.0,200.0){\circle{10.0}}
  \put(200.0,0.0){\line(0,6){400.0}} 
  \put(200.200,-20.200){Y-Achse} 
  \put(200.200,20.200){-6}
  \put(200.200,50.200){-5}
  \put(200.200,80.200){-4}
  \put(200.200,110.200){-3}
  \put(200.200,140.200){-2}
  \put(200.200,170.200){-1}
  \put(200.200,410.200){Y-Achse} 
  \put(200.200,380.200){+6}
  \put(200.200,350.200){+5}
  \put(200.200,320.200){+4}
  \put(200.200,290.200){+3}
  \put(200.200,260.200){+2}
  \put(200.200,230.200){+1}
 \end{picture}
\end{document}

Mit der ensprechenden Ausgabe:

Beispiel Kordinatensystem für X & Y Achse mit +/- Bereich.

Ja das Bild bzw. die Zeichnung ist nicht perfekt, aber das muss sie auch nicht sein. Mit dem hier beschriebenem soll man in der Lage sein einfache horizontale und vertikale linien und Pfeile zeichnen zu können. Vl. findet sich ja einer von euch Lesern der es perfekt hinbekommt...

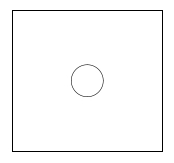
Kreis

Einen einfachen kreis kann man mit dem Befehl \circle{25.0} erzeugen. In den geschweiften Klammern, wird der Durchmesser des Kreises angegeben. Dieser kann frei gewählt werden. Am besten verwendet man hier wieder eine Picture Umgebung deren Grösse wir festlegen. In diesem Beispiel nehme ich einfach mal 100 x 100. Wenn Wir dann einen Kreis zeichenen der einen Durchmesser von 25 hat, ist das ein viertel der grafischen Picture Umgebung und somit recht gross und deutlich anzusehen. Damit man die Picture Umgebung ebenfalls sehen kann, verwende ich hier zusätzlich noch eine fbox die wir weiter oben bereits kennengelernt haben und immer wieder praktisch auch als kleines Helferlein ist. Nach einer Vertigstellung kann die fbox ja wieder entvernt werden wen man keinen Rahmen mehr möchte.

\begin{document}

 \fbox{

  \begin{picture}(100,100)

\put(50.0,50.0){\circle{25.0}}

  \end{picture}

 }
\end{document}

Beispiel Kreis in einer Picture Umgebung unter LaTeX.

Würfel Beispiel

Hier möchte ich mal ein Beispiel für einen Würfel zeigen.

\begin{document}
 \fbox{
  \begin{picture}(100,100)
   \put(50.0,50.0){\circle*{25.0}}
   \put(75.0,75.0){\circle*{25.0}}
   \put(25.0,25.0){\circle*{25.0}}
  \end{picture}
 }
\end{document}

Beispiel Würfel in einer Picture Umgebung unter LaTeX.

Hier noch ein weiterer Würfel:

\begin{document}
 \fbox{
  \begin{picture}(100,100)
   \put(50.0,50.0){\circle*{25.0}}
   \put(75.0,75.0){\circle*{25.0}}
   \put(25.0,25.0){\circle*{25.0}}
   \put(25.0,75.0){\circle*{25.0}}
   \put(75.0,25.0){\circle*{25.0}}
  \end{picture}
 }
\end{document}

Beispiel Würfel in einer Picture Umgebung unter LaTeX.

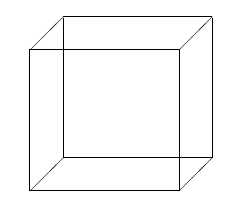
3D Würfel

In diesem Beispiel habe ich versucht einen Würfel in 3D darzustellen, ich hoffe mir ist es halbwegs gelungen.

\begin{document}
 \fbox{
  \begin{picture}(100,100)
   \put(50.0,50.0){\circle*{25.0}}
   \put(75.0,75.0){\circle*{25.0}}
   \put(25.0,25.0){\circle*{25.0}}
   \put(25.0,75.0){\circle*{25.0}}
   \put(75.0,25.0){\circle*{25.0}}
   \put(-6.0,102.0){\line(1,1){25.0}} 
   \put(106.0,102.0){\line(1,1){25.0}} 
   \put(106.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,128.0){\line(1,0){112.0}}
   \put(131.0,22.0){\line(0,1){105.0}}
  \end{picture}
 }
\end{document}

Beispiel 3D Würfel in einer Picture Umgebung unter LaTeX.

Hier noch ein weiterer kleiner 3D Würfel:

3D Würfel Beispiel

\begin{document}
 \fbox{
  \begin{picture}(100,100)
   \put(-6.0,102.0){\line(1,1){25.0}} 
   \put(106.0,102.0){\line(1,1){25.0}} 
   \put(106.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,128.0){\line(1,0){112.0}}
   \put(131.0,22.0){\line(0,1){105.0}}
   \put(-6.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,22.0){\line(1,0){112.0}}
   \put(19.0,22.0){\line(0,1){105.0}}
  \end{picture}
 }
\end{document}

Beispiel 3D Würfel in einer Picture Umgebung unter LaTeX.

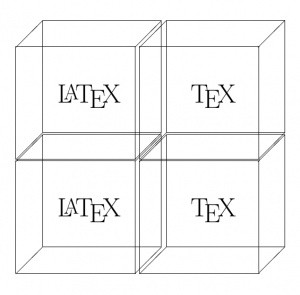
Letzten Beispiel:

\begin{document}
 \fbox{
  \begin{picture}(100,100)
   \put(-6.0,102.0){\line(1,1){25.0}} 
   \put(106.0,102.0){\line(1,1){25.0}} 
   \put(106.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,128.0){\line(1,0){112.0}}
   \put(131.0,22.0){\line(0,1){105.0}}
   \put(-6.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,22.0){\line(1,0){112.0}}
   \put(19.0,22.0){\line(0,1){105.0}}
   \put(33.0,50.0){\begin{Huge}\LaTeX\end{Huge}}
  \end{picture}
 }
 \fbox{
  \begin{picture}(100,100)
   \put(-6.0,102.0){\line(1,1){25.0}} 
   \put(106.0,102.0){\line(1,1){25.0}} 
   \put(106.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,128.0){\line(1,0){112.0}}
   \put(131.0,22.0){\line(0,1){105.0}}
   \put(-6.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,22.0){\line(1,0){112.0}}
   \put(19.0,22.0){\line(0,1){105.0}}
   \put(42.0,50.0){\begin{Huge}\TeX\end{Huge}}
  \end{picture}
 }

 \fbox{
  \begin{picture}(100,100)
   \put(-6.0,102.0){\line(1,1){25.0}} 
   \put(106.0,102.0){\line(1,1){25.0}} 
   \put(106.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,128.0){\line(1,0){112.0}}
   \put(131.0,22.0){\line(0,1){105.0}}
   \put(-6.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,22.0){\line(1,0){112.0}}
   \put(19.0,22.0){\line(0,1){105.0}}
   \put(33.0,50.0){\begin{Huge}\LaTeX\end{Huge}}
  \end{picture}
 }
 \fbox{
  \begin{picture}(100,100)
   \put(-6.0,102.0){\line(1,1){25.0}} 
   \put(106.0,102.0){\line(1,1){25.0}} 
   \put(106.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,128.0){\line(1,0){112.0}}
   \put(131.0,22.0){\line(0,1){105.0}}
   \put(-6.0,-4.0){\line(1,1){25.0}} 
   \put(19.0,22.0){\line(1,0){112.0}}
   \put(19.0,22.0){\line(0,1){105.0}}
   \put(42.0,50.0){\begin{Huge}\TeX\end{Huge}}
  \end{picture}
 }
\end{document}

Beispiel 3D Würfel in einer Picture Umgebung unter LaTeX.

Komando Definition

Ab und an hat man etwas grösseres oder etwas das sich sehr oft wiederholt und man möchte dieses nicht immer wieder schreiben müssen. Für so einen Fall, können wir ein eigenes neues Komando definieren das dann die gewünschten Zeilen einfügt oder ausführt.

Angenommen ich schreibe einen Text in dem ich zum Beispiel sehr oft eine Nummer oder einen langen Namen schreiben muss, dann kann ich mir das Leben mit dem Befehl \newcommand etwas vereinfachen.

\begin{document}
 \newcommand{\n}{0100101}
  Nun kann ich meinen Text schreiben in dem ich nicht mehr 
  die Nummer \n ~schreiben muss.
\end{document}

Wie im Beispiel zu sehen, erstellen wir einen neuen Befehl oder ein neues Komando \n an jeder Stelle im Quelltext wo das neue Komando steht wird dann die entsprechende Aktion oder Anweisung durchgeführt. Un unserem Fall sagen wir das \n eine Nummer {0100101} ist welche wir nicht immer wieder neu schreiben wollen. Nun wird wie im Beispiel zu sehen, an der Stelle wo unser neues Komando steht die Nummer ausgegeben.

Beispiel Newcommand unter LaTeX.

Mathematische Formeln

Umgebungen für mathematische Formeln

Formeln im Fließtext

Um eine Formel im Text zu setzten gibt es die $Formel$ Umgebung.

Beispiel:

Dieser Bruch $\frac{1}{x^2}$ passt genau in eine Zeile.

Ein mit Latex gesetzter Bruch im Fließtext

Formeln werden in dieser Umgebung etwas zusammengestaucht. Dadurch leidet etwas die Schönheit der Formel. Wenn man mehr Platz hat, nimmt man besser eine Umgebung für abgesetzte Formeln.

Abgesetzte Formeln

Hier gibt es eine ganze Reihe von Umgebungen. Zum Beispiel:

\begin{displaymath}
  Formel
\end{displaymath}

\begin{equation} 
  Formel
\end{equation} 

\begin{eqnarray}
  Formel
\end{eqnarray} 

Es werden noch zahlreiche weitere Umgebungen durch das Paket amsmath bereitgestellt. Man kann es durch die Anweisung

\usepackage[optionale Parameter]{amsmath}

in der Präambel einbinden. Das Paket enthält einige Ergänzungen zum Latexstandard.

Diese Umgebungen wirken alle leicht unterschiedlich. Die equation-Umgebung etwa arbeitet genau wie die displaymath-Umgebung, setzt aber zusätzliche Nummerierungen an die Formeln. Die eqnarray-Umgebung eignet sich zum Setzen von Gleichungssystemen. Welche Umgebung man verwendet, hängt nicht zuletzt auch vom persönlichen Geschmack ab. In dieser Einführung werden wir uns auf die Umgebung

\begin{displaymath}
  Formel
\end{displaymath}

beschränken. Diese Umgebung kann man auch kürzer

\[ Formel \]

schreiben.

Beispiele

Brüche

Um einen Bruch zu setzen, gibt es das Kommando \frac{Zaehler}{Nenner}

Beispiel:

\begin{displaymath}
 \frac{1}{1+1} = \frac{1}{2}
\end{displaymath}

Ein mit displaymath gesetzter Bruch

Wurzeln

Um eine Wurzel zu setzen, gibt es das Kommando \sqrt[..]{..} Beispiel: Die vierte Wurzel aus 81 ist 3.

\begin{displaymath}
  \sqrt[4]{81}=3
\end{displaymath}

Die vierte Wurzel aus 81.

Eine quadratische Wurzel setzt man so: \sqrt{..}

\begin{displaymath}
  \sqrt{2}=1,4142
\end{displaymath}

Die Quadratwurzel aus 2.

Das Summenzeichen

Das Summenzeichen wird duch den Befehl \sum gesetzt.

\begin{displaymath}
  \sum
\end{displaymath}

Summenzeichen

Hoch- und Tiefstellen

Mit dem ^ wird etwas hochgestellt. Mit dem _ wird etwas tiefgestellt. Soll mehr als ein Zeichen hoch- oder tiefgestellt werden, müssen diese Zeichen in geschweifte Klammern { } gesetzt werden.

Beispiel:

\begin{displaymath}
  \sum_{i=1}^n
\end{displaymath}

Summe von 1 bis n

Vergisst man die Klammern um {i=1}, so wie im folgenden Beispiel, passiert das:

\begin{displaymath}
  \sum_i=1^n
\end{displaymath}

Klammerung vergessen

Integrale

Das Integralzeichen erhält man duch den Befehl \int

Beispiel:

\begin{displaymath}
  \int_a^bf(x)dx
\end{displaymath}

Das Integral

Das Produktzeichen

Das Produktzeichen erhält man durch den Befehl \prod

Beispiel:

\begin{displaymath}
  \prod_{i=1}^3 i = 1*2*3 = 3!
\end{displaymath}

Gebrauch des Produktzeichens

Binomialkoeffizienten

Die Binomialkoeffizienten n über k erhält man durch den Befehl {n \choose k}

Beispiel:

\begin{displaymath}
  {n \choose k} = \frac{n!}{k!(n-k)!}
\end{displaymath}

Die Binomialkoeffizienten

Limes

Der Limes wird durch das Kommando \lim gesetzt. Der Pfeil nach rechts wird durch das Kommando \rightarrow gesetzt. Das "Unendlich"-Zeichen wird durch das Kommando \infty gesetzt.

\begin{displaymath}
  \lim_{x\rightarrow\infty} \frac{1}{x} = 0
\end{displaymath}

Grenzwert 1/x

Klammerungen in Formeln

Normale Klammern (die \left \right Umgebung)

Klammern setzt man am besten mit der \left \right Umgebung, denn dann passt sich die Größe der Klammern an die Größe der Formeln an. Die Klammern werden direkt nach \left oder \right gesetzt. Man kann alle möglichen Klammern nehmen. Etwa (), [], {}, <>. Auch den senkrechten Strich | kann man verwenden. Man muß die Klammern nicht paarweise verwenden. Auch (} ist möglich. Und dies ][ ist möglich. Die Befehle \left \right müssen immer paarweise vorkommen. Will man aber etwa nur eine sich öffnende Klammer haben, so setzt man nach dem \right einen Punkt. \right. (Punkt)

Hinweis: Wenn man geschweifte Klammern {} verwenden will, muß man ein \ voranstellen.

Beispiel: Eine runde und eckige Klammer um unser Integral.

\begin{displaymath}
 \left( \int_a^bf(x)dx  \right>
\end{displaymath}

Verschiedene Klammern um ein Integral

Ein weiteres Beispiel für die \left \right Umgebung findet man im Abschnitt 1.16.5.2 Matrizen.

Klammerung von unten (\underbrace)

Der Befehl \underbrace{} klammert von unten nach oben.

Beispiel 1:

\begin{displaymath}
  \underbrace{a+b}
\end{displaymath}

Klammer von unten

Beispiel 2: (Rechenaufgabe des Gauss)

\begin{displaymath}
 \sum_{i=1}^{100} i = 1+2+\dots+99+100 = 
 \underbrace{1+100}_{101} +  \underbrace{2+99}_{101} + \dots +\underbrace{50+51}_{101}
 = 50*101 = 5050
\end{displaymath}

Die Rechenaufgabe des Gauss

Klammerung von oben (\overbrace)

Der Befehl \overbrace{} klammert von oben nach unten.

Beispiel:

\begin{displaymath}
  \overbrace{a+b}
\end{displaymath}

Klammer von oben

Horizontale Abstände in Formeln

Abstände

Sehr selten ist man mit den von LaTeX gewählten Abständen nicht zufrieden. Um diese Abstände zu vergrößern, gibt es unter anderem folgende Befehle:

\, (kleiner Abstand)

\: (etwas größerer Abstand)

\quad (großer Abstand)

\qquad (2 * quad)

Darüber hinaus gibt es den Befehl \hspace{abstand}. Hier kann man den Abstand zum Beispiel in pt (Breite eines Punktes), mm oder cm angeben. Durch die Anweisung \hspace{2cm} wird also ein 2 cm breiter horizontaler Abstand eingefügt.

Beispiel (Dichte der Normalverteilung)

(Siehe Kleine Enzyklopädie Mathematik 2. Auflage 1984 Verlag Harry Deutsch. Seite 642)

Die Dichte der Normalverteilung kann man dann durch folgenden Code setzen:

\begin{displaymath}
 p(x) = \frac{1}{a\sqrt{2\pi}}  e^{-\frac{(x-b)^2}{2a^2}}
\end{displaymath}

Und hier das Gleiche. Ein kleiner Abstand wurde eingefügt.

\begin{displaymath}
 p(x) = \frac{1}{a\sqrt{2\pi}} \,  e^{-\frac{(x-b)^2}{2a^2}}
\end{displaymath}

Dichte der Normalverteilung

Ob man es wirklich für nötig hält, hier einen Abstand einzufügen, ist natürlich Geschmackssache. Ein weiteres Beispiel für zusätzlich eingefügten Abstand findet man im gleich folgenden Beispiel Indikatorfunktion. Dort ist es aber wirklich nötig.

Bedingte Funktionen und Matritzen (Arrays in Formeln)

Bedingte Funktionen

Um eine bedingte Funktion zu setzten, benötigt man die Umgebung

\begin{displaymath}
  \begin{array}{Spalten}
    Tabelle
  \end{array}
\end{displaymath}

Mit dieser Umgebung setzen wir eine Tabelle. Das & Zeichen trennt die Spalten. Für eine 2-Spaltige Tabelle geben wir hier für Spalten cc ein. Das zeigen wir gleich am Beispiel Indikatorfunktion. Wir haben hier eine sich öffnende linke Klammer. Die rechte Klammer wurde unsichtbar gemacht (der Punkt nach right). Zeilen schließt man durch \\ ab.

Beispiel: (Indikatorfunktion)

\begin{displaymath}
 1_{[0,1]}(x) = 
  \left\{ \begin{array}{cc}
                1 & falls \quad x \in [0,1]  \\
                0 & sonst  
          \end{array} 
  \right.
\end{displaymath}

Indikatorfunktion

Zwischen \begin{array}{cc} und \end{array} wird hier eine 2-Spaltige Tabelle gesetzt. Die Spalten werden durch das & Zeichen getrennt. In der ersten Spalte stehen die 1 und die 0, in der zweiten Spalte stehen die Bedingungen.

Matrizen

Auch für Matrizen verwenden wir die array-Umgebung. Für eine 3x3-Matrix benötigen wir 3 Spalten. Deshalb setzen wir 3 c ein. Auch hier werden Zeilen durch \\ getrennt. Die Spalten werden durch das & Zeichen getrennt. Es ist auch noch ein schönes Beispiel für die \left \right Umgebung. Hier ist die Matrix:

\begin{displaymath}
  A = 
    \left( \begin{array}{ccc}
                1 & 2 & 3  \\
                4 & 5 & 6  \\
                7 & 8 & 9  
            \end{array} 
    \right)
\end{displaymath}

3x3-Matrix

LaTeX: (1.) Einleitung - (2.) Schnellkurs - (3.) Teil 1 - Grundlagen - (4.) Teil 2 - Grundlagen - (5.) Fortgeschrittene - (6.) Literaturverzeichnisse - (7.) Zeichen und Symbole - (8.) LaTeX Distributionen - (9.) LaTeX Links

---

zurück zu Office