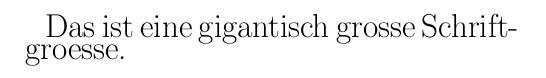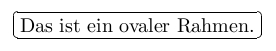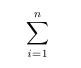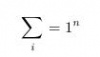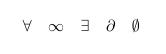LaTeX All: Unterschied zwischen den Versionen
Yehudi (Diskussion | Beiträge) (angepasst) |
Yehudi (Diskussion | Beiträge) (angepasst) |
||
| Zeile 11: | Zeile 11: | ||
{{:LaTeX/Zeichen und Symbole}} | {{:LaTeX/Zeichen und Symbole}} | ||
| − | {{: | + | {{:LaTeX/Distributionen}} |
Version vom 23. Juli 2007, 07:03 Uhr
| LaTeX: (1.) Einleitung - (2.) Schnellkurs - (3.) Teil 1 - Grundlagen - (4.) Teil 2 - Grundlagen - (5.) Fortgeschrittene - (6.) Literaturverzeichnisse - (7.) Zeichen und Symbole - (8.) LaTeX Distributionen - (9.) LaTeX Links |
| (Lamports LaTeX) | |
|---|---|
 | |
| Basisdaten | |
| Entwickler: | Dr. Leslie Lamport |
| Aktuelle Version: | LaTeX 2ε |
| letzte Veröffentlichung: | |
| Betriebssystem: | Linux, BSD, Mac OS X, Unix, Windows |
| Kategorie: | Schriftsatz |
| Lizenz: | Frei verfügbar |
| Deutschsprachig: | |
| Webseite: | http://www.latex-project.org/ |
Inhaltsverzeichnis
- 1 Einleitung
- 2 Schnellkurs
- 3 Schnellkurs mit Kile
- 4 Grundlagen Teil 1
- 5 Grundlagen Teil 2
- 5.1 Weiteres Seitenlayout
- 5.2 Mehrspaltiger Text
- 5.3 Textrahmen
- 5.4 Spezielle Rahmen
- 5.5 Grafik einbinden
- 5.6 Tabellen
- 5.7 Linien
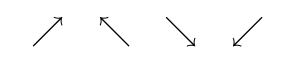
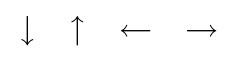
- 5.8 Pfeillinien
- 5.9 Kordinatensystem
- 5.10 Picture Umgebung
- 5.11 Objekt Positionieren
- 5.12 Beispiel Zeichnung
- 5.13 Kreis
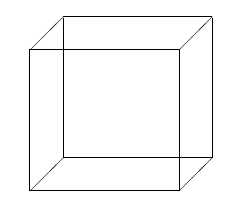
- 5.14 3D Würfel
- 5.15 Komando Definition
- 5.16 Querformat (Verschiedene Möglichkeiten zur Einstellung von Seitenrändern)
- 5.17 Mathematische Formeln
- 6 Fortgeschrittene
- 6.1 Für was ?
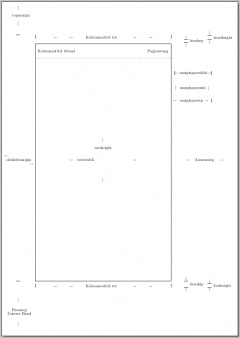
- 6.2 Seitenaufbau
- 6.3 Satzspiegel
- 6.3.1 Konstruktionsverfahren
- 6.3.2 Welches Konstruktionsverfahren
- 6.3.3 Satzspiegel der Standartklassen
- 6.3.4 Dimensionsparamter
- 6.3.4.1 Höhe Satzspiegel
- 6.3.4.2 Breite Satzspiegel
- 6.3.4.3 Kopfsteg
- 6.3.4.4 Linker Rand Einseitig
- 6.3.4.5 Linker Rand Zweiseitig
- 6.3.4.6 Seitenkopf zum Satzspiegel
- 6.3.4.7 Seitenkopfbereich
- 6.3.4.8 Seitenfuß zum Satzspiegel
- 6.3.4.9 Seitenfußbereich
- 6.3.4.10 Marginalie zum Satzspiegel
- 6.3.4.11 Marginalie Breite
- 6.3.4.12 Marginalie zur Randnotiz
- 6.3.4.13 Abstand zwischen Absatz
- 6.3.4.14 Zeilendurchschuss
- 6.3.4.15 Marginalien Seite
- 6.3.5 Layout Vergleich
- 6.3.6 Automatische Satzspiegelkonstruktion
- 6.4 Schriften
- 6.5 Mehr Mathematisches
- 7 Zeichen und Symbole
- 8 Welches LaTeX ?
- 9 Installation
- 10 LaTeX Distributionen
Einleitung
Mit diesem LaTeX Kompendium soll ein einfacher Einstieg sowie ein Schnellstart in LaTeX ermöglicht werden. Es wird versucht, auf lange technische Ausführungen zu verzichten, da diese eh von kaum einem Anwender gebraucht werden. Das Ziel sollte sein, den Anwender in die Lage zu versetzen, die alltäglichen Office Aufgaben (Hausarbeiten, Seminare, Briefe, Etiketten, Bücher, Berichte, etc.) mit LaTeX bewältigen zu können.
Auf spezielle LaTeX Erweiterungen und Zusatzprogramme wird hier bewusst verzichtet, da diese nicht zu einem Schnellstart Einstieg gehören.
Was ist LaTeX ?
![]() wird üblicherweise in ganz normalem Text als LaTeX geschrieben.
wird üblicherweise in ganz normalem Text als LaTeX geschrieben.
Wenn wir hier von LaTeX sprechen, ist weder der Milchsaft des Kautschukbaumes, noch die Latexfarbe oder das Bekleidungsmaterial Latex gemeint.
Mit LaTeX beziehen wir uns auf ein Softwarepaket welches im Jahr 1984 von Dr. Leslie Lamport (Mathematiker, Informatiker und Programmierer) entwickelt wurde. Dieses Softwarepaket ist dank seiner Macros eine Vereinfachung des Textsatzsystemes ![]() , dessen Komponente im Jahr 1986 Donald Ervin Knuth geschaffen hat. Donald E. Knuth ist emeritierter Professor für Informatik und war beim Schreiben seiner Buchreihe "The Art of Computer Programming" (TAOCP) mit der typographischen Qualität seiner Bücher unzufrieden. Er beschloss, die Sache selbst in die Hand zu nehmen und traf viele wichtige Schriftdesigner, wie beispielsweise Hermann Zapf, von denen er sehr viele Dinge lernte durfte. Letztenendes hat das TeX Projekt über 10 Jahre seiner Zeit in Anspruch genommen. Da Knuth es nun als abgeschlossen ansieht, finden nur noch Fehlerbereinigungen statt.
Das TeX System wird daher heute nur noch von ein Paar hartgesottenen Anwendern genutzt. Der Name LaTeX setzt sich aus (La)mport und TeX zusammen.
, dessen Komponente im Jahr 1986 Donald Ervin Knuth geschaffen hat. Donald E. Knuth ist emeritierter Professor für Informatik und war beim Schreiben seiner Buchreihe "The Art of Computer Programming" (TAOCP) mit der typographischen Qualität seiner Bücher unzufrieden. Er beschloss, die Sache selbst in die Hand zu nehmen und traf viele wichtige Schriftdesigner, wie beispielsweise Hermann Zapf, von denen er sehr viele Dinge lernte durfte. Letztenendes hat das TeX Projekt über 10 Jahre seiner Zeit in Anspruch genommen. Da Knuth es nun als abgeschlossen ansieht, finden nur noch Fehlerbereinigungen statt.
Das TeX System wird daher heute nur noch von ein Paar hartgesottenen Anwendern genutzt. Der Name LaTeX setzt sich aus (La)mport und TeX zusammen.
Nun wissen wir was mit LaTeX gemeint ist und wie es geschrieben wird, fehlt also nur noch die richtige Aussprache.
Das X ist ein χ aus dem griechischen Alphabet, genau genommen ist es der 22te Buchstabe. Bei uns hier im deutschen Raum wird dieses grichische X als ch ausgesprochen. Ein Wort an welches sich dieses ch bei der Aussprache anlehnt wäre zum Beispiel: "Techniker".
Ähnlich ist es bei der Aussprache von TeX, welches bei uns im deutschen Sprachraum als Tech ausgesprochen werden müsste.
Eigenschaften
Das Textsatzsystem LaTeX, welches eine Erweiterung von TeX darstellt, eignet sich besonders gut für das Erstellen von wissenschaftlichen technischen Texten in Buchdruckqualität. Es ist extrem leistungsfähig und im Vergleich zu TeX recht einfach in der Handhabung, da TeX eher etwas für Profis aus dem Programmierbereich ist. LaTeX ist durch seine Zwischenebene im Vergleich zu TeX sehr benutzerfreundlich, da man keine Programmierkenntnisse benötigt.
Man kann so wunderbar die TeX Möglichkeiten nutzen, um anspruchsvolle Texte, Tabellen oder Formeln in einer sehr guten Qualität zu erstellen.
Durch die Standardeinstellungen von LaTeX werdem dem Anwender Formatierungen auf sehr hohem Niveau geboten, da hier ein großes Fachwissen von professionellen Druckern sowie Grafikern, Schriftsetzern, Typografen und Kaligrafen eingeflossen ist.
Verwendung
Heute wird LaTeX von vielen großen Verlagen für den Buchdruck verwendet, da der mathematische Formelsatz eine der größten Stärken von LaTeX ist. Desweiteren kommt es häufig an Universitäten und Fachhochschulen zum Einsatz. Durch die Möglichkeit der Erweiterung um zusätzliche Pakete für bestimmte Fachbereiche wird es auch von Unternehmen eingesetzt.
Um nur ein Paar wenige Fachbereiche zu nennen:
- Kataloge
- Bücher
- Briefe
- Diplomarbeiten
- Doktorarbeiten (Dissertationen)
- Bibeltexte
- Literaturverzeichnisse
- Notensatz
- Bibliografien
- Stichwortverzeichnisse
- Präsentationen
- Manuskripte
- Etiketten, Labels, Cover
- Artikel
- Visitenkarten
Es gibt extrem viele Zusatzpakete für alle nur erdenklichen Themengebiete.
Entwicklungsgeschichte
Der Schöpfer Leslie Lamport entwickelte sein LaTeX aus der damaligen verfügbaren TeX Version 82. Erst im Dezember 1991 wurde LaTeX 2.09 um weitere Sprachen als nur Englisch erweitert. Mit der Erweiterung um die deutsche Sprache wurden auch die Umlaute (ä, ö, ü) hinzugefügt. Desweiteren werden Dinge wie Chapter im deutschen Inhaltsverzeichnis als Kapitel geschrieben. Derzeit gibt es das LaTeX 3-Projekt, welches versucht die nächste Version von LaTeX zu schaffen.
Entwicklungsversionen
- 05/1985 - LaTeX 2.09
- 06/1994 - LaTeX 2ε
Technik
LaTeX baut auf TeX auf, bei dem es sich technisch gesehen um einen Interpreter handelt der viele fest eingebaute primitives kennt und einen sehr komplexen Mechanismus zur Definition von Makros bereitstellt. Es wird nach einem ausgeklügelten Optimierungsverfahren gearbeitet, bei dem in jedem Textsatz der Absatz sowie die Silbentrennung etc. gleichzeitig bestimmt werden. Die Optimalen Seitenumbrüche werden dann durch einen bestimmten Algorithmus erstellt. Das Optimierungsverfahren arbeitet nach bestimmten penalties.
Die Zeilen und Seitenumbrüche werden nach vielen Parametern, Registern, Regeln und elastischen Längen festgelegt. LaTeX wie auch TeX kommen mit enorm wenig Ressourcen aus und sind daher auch auf älteren Systemen lauffähig. Desweiteren sind sie so ausgereift, dass auch beim Arbeiten mit extrem großen und komplexen Dokumenten keine Instabilität auftritt.
Entwicklungsumgebung
LaTeX Dokumente werden in einer Entwicklungsumgebung erstellt, was auch mit einem ganz einfachen Text oder Komandozeileneditor funktionieren würde. Der große Vorteil von LaTeX Entwicklungsumgebungen ist es, dass Programme die eigens für das Erstellen von LaTeX Dokumenten geschrieben bzw. angepasst wurden, dem Anwender sehr viel Arbeit bei der Dokumentenerstellung abnehmen. Sehr häufig gebrauchte Befehle, wie beispielsweise für die Schriftform oder Farbe, den Zeilenumbruch oder Tabellen, sind so über eine grafische Oberfläche bzw. eine GUI mit der Maus erreichbar. Desweiteren werden einem zum Beispiel Funktionen geboten, wie die Möglichkeit einer Dokumentenvorschau sowie Rechtschreibprüfungen, Autovervollständigungen etc. wie z.B. bei Kile, der KDE LaTeX Entwicklungsumgebung.
Grundprinzip
Bei LaTeX handelt es sich nicht um ein gewöhnliches Textverarbeitungsprogramm wie MSOffice oder OpenOffice, bei denen man bereits bei der Eingabe der Daten bzw. des Textes auf dem Bildschirm das spätere Ergebnis sieht. Einfache Textverarbeitungsprogramme, wie man sie kennt, werden aus diesem Grunde auch WYSIWYG Programme genannt. WYSIWYG Steht für (what you see is what you get). Übersetzt würde das in etwa heißen: "Du siehst was du erstellst". Unter LaTeX ist das etwas anders, hier werden in dem LaTeX Dokument Formatierungen, Überschriften, Farben, Größen etc. textuell ausgezeichnet. D.h. Es werden Befehle mit in den zu erstellenden Text geschrieben, welche diesen Text dann entsprechend formatieren. Da wir hier mit bestimmten LaTeX Befehlen arbeiten, schreiben wir also eine Quelldatei, welche, wie der Name schon sagt, den Quelltext (unseren Text und die LaTeX Befehle) enthält. Um nach der Fertigstellung des Quelltextes unser fertiges Dokument zu erhalten, muss dieser Text kompiliert werden. Erst nach dem Kompiliervorgang erhalten wir eine Datei (meist im DVI - Device independent file format), welches wir mit einem entsprechenden Werkzeug betrachten, drucken oder in irgendeiner Art und Weise weiterverarbeiten können.
Plattformunabhänigkeit
Wie schon TeX, so ist auch LaTeX plattformunabhängig, was bedeutet, dass es keine Rolle spielt, welches Betriebsystem oder welche Hardware vorhanden ist. Ein unter Linux auf x86 Hardware erstelltes LaTeX Quelldokument sieht nach dem Kompilieren genauso aus, wie wenn man es unter einem Mac OS X auf PPC (PowerPC) Hardware gemacht hätte. Nach der Installation von LaTeX auf dem eigenen System, ist man z.b. nicht auf die systemeigenen Schriftarten angewiesen, LaTeX bringt bereits selbst sehr hochwertige Schriftformen mit.
Linux / BSD / Unix Systeme
- Kile Der KDE LaTeX Editor.
- Winefish Winefish LaTeX Editor für Gnome.
- Lyx Multiplattform - Editor.
- Vim Plattformunabhängiger Editor.
- Emacs Vielseitiger Texteditor, fürs Programmierer oder zum LaTeX schreiben.
Mac OS X
- TeXShop Ein sehr weit verbreiteter Editor unter Mac OS X.
- iTeXMac Ein weiteres Mac OS LaTeX Entwicklungswerkzeug.
Schnellkurs
Nachdem wir nun die oberen Punkte aufmerksam durchgelesen haben und in etwa wissen, was LaTeX ist, was man damit alles machen kann usw., wollen wir nun unser erstes mit Hilfe von LaTeX erstelltes Dokument in Angriff nehmen.
Dokumentenstruktur
Ein LaTeX Dokument hat eine ganz bestimmte Dokumentenstruktur, welche hier kurz erklärt werden soll. Die Dokumentenstruktur setzt sich im Großen und Ganzen aus zwei Teilen zusammen.
- Präambel
- Dokumenteninhalt
Präambel
In der Präambel, dem ersten Teil unseres Dokuments, werden sämtliche Dokumenteneinstellungen festgelegt, sowie weitere Zusatzpakete bzw. Macropakete geladen. D.h. wir legen in der Präambel unsere Dokumentenart fest, welche durch die Dokumentenklasse gekennzeichnet wird. Festgelegt wird die Dokumentenklasse folgendermaßen:
\documentclass[Optionen]{Dokumentklasse}[Versionsdatum]
Papierformat
Hierzulande ist es üblich, dass man für Briefe, Dokumente etc. das DIN A4 Papierformat verwenden.
\documentclass[a4paper]
Weitere Formate die unter LaTeX verwendet werden können sind zum Beispiel:
- a4paper
- a5paper
- b5paper
- letterpaper
- legalpaper
- executivepaper
Punktgröße
Wir möchten für unser Dokument nicht nur das Papierformat wählen, sondern auch noch die Standardschrift mit einer bestimmten Punkgröße. Zur Information: ein Punkt, hier abgekürzt als (pt), entspricht etwa einer Größe von 0.35 mm. Wir wählen in unserem ersten Dokument eine 11 Punkt hohe Schrift.
\documentclass[a4paper,11pt]
Punktgröße 10
Eine 10 Punkt große Schrift wird mit der Option [10pt] angegeben.
Punktgröße 11
Eine 11 Punkt große Schrift wird mit der Option [11pt] angegeben.
Punktgröße 12
Eine 12 Punkt große Schrift wird mit der Option [12pt] angegeben und ist in etwa das, was man von einer Schreibmaschine her kennt.
Keine Punktgröße
Wird keine Punktgröße angegeben, so nimmt LaTeX eine [10pt] (10 Punkt) hohe Standardschrift, welche im Buchdruck üblich ist.
Dokumentenklasse
Als Dokumentenklasse gibt es div. Auswahlmöglichkeiten, zu diesen folgende gehören:
- article
- book
- report
- letter
Wir möchten in unserem Dokument die Klasse "article" verwenden und passen den Eintrag entsprechend an:
\documentclass[a4paper,11pt]{article}
Article
Article ist zum Beispiel für folgende Dinge geeignet:
- Seminararbeiten
- Vorträge
- Kleine Berichte
- Einladungen
- Beschreibungen
Report
Report ist zum Beispiel für diese Dinge geeignet:
- Skripte
- Grössere Berichte
- Dokumente welche mehrere Kapitel beinhalten
Book
Wie der Name schon sagt ist dies die zu wählende Klasse wenn man ein Buch schreiben möchte.
- Bücher
Letter
Letter eignet sich sehr gut für Briefe.
Versionsdatum
Das Versionsdatum kann mit angegeben werden, um zu verhindern, dass der LaTeX Quellcode mit einer zu alten LaTeX Version kompiliert wird. Diese Funktion wird in der Praxis zwar sehr selten gebraucht, sollte aber der Vollständigkeit halber hier ebenfalls erwähnt werden.
Zusatzpakete
Ein weiterer wichtiger Teil, welcher zur Präambel gehört, ist die Möglichkeit des Hinzufügens von z.B. weiteren Zusatzpaketen, welche man für die Arbeit mit LaTeX benötigt, um die Entsprechende Aufgabe zu bewältigen. Hier ein kleines Beispiel der Grundstruktur des Befehles \usepackage:
\usepackage[Optionen]{Ergänzungspaket}[Versionsdatum]
Zusatzpaket Option
Hier wird die gewünschte Option mit angegeben, welche man verwenden möchte. Ein Beispiel hierfür wäre ngerman.
\usepackage[ngerman]
Die Option ngerman ist in diesem Beispiel für die Unterstützung der deutschen Sprache verantwortlich.
Es sollte hierbei beachtet werden, das man die eingegebenen Option nur nutzen kann, wenn diese vom Ergänzungspaket auch unterstützt werden.
Zusatzpaket Ergänzungspaket
Wie immer folgt zuerst ein kleines Beispiel:
\usepackage[ngerman]{babel}
In diesem Beispiel ist das Ergänzungspaket babel, welches in den geschweiften Kammern steht und für die Sprachumschaltung zuständig ist.
Zusatzpaket Versionsdatum
Beim Versionsdatum möchte ich auf den Punkt 1.1.1.4 verweisen, da es die selbe Funktion, wie bereits oben beschrieben wurde, hat.
Dokumenteninhalt
Im Dokumenteninhalt steht unser eigentlicher Text, welchen wir als Autor verfassen. Zudem werden dort unsere Formatbefehle, mit deren Hilfe wir unseren Text entsprechend gestalten, eingestellt.
Der eigentliche Text
Der Dokumenteninhalt, d.h. unser eigentlicher Text, welchen wir verfassen wollen, steht zwischen den Anweisungen:
\begin{document}
und endet vor der Anweisung:
\end{document}
Ein kleines Beispiel wäre also:
\begin{document}
Das ist unser Text welchen wir verfassen.
\end{document}
Befehle & Anweisungen
Wie bereits in den oberen Beispielen zu sehen war, beginnen Befehle oder Anweisungen mit einem so genannten Backslash (\).
Beispiel:
\end{document}
Kommentare
Kommentare sollen nicht in der fertigen Ausgabe, dem fertigen Dokument, erscheinen. Kommentare werden durch das % Zeichen eingeleitet. Das % Zeichen und alles was danach in derselben Zeile steht, erscheint nicht in der Ausgabe.
Beispiel:
\documentclass[a4paper,10pt]{article}
%Ich bin der erste Kommentar.
\begin{document}
Heute ist ein toller Tag! %Ich bin der zweite Kommentar.
% Ich bin der dritte Kommentar.
Alles ist ganz wunderbar! %Ich bin der vierte Kommentar.
% Ich bin der fünfte Kommentar.
\end{document}
Und die Ausgabe:
Wenn man möchte, dass das % Zeichen in der Ausgabe erscheint, dann muß man das extra anweisen, und zwar indem ein Backslash davor gesetzt wird: \%. Jetzt würde das % Zeichen im Text erscheinen.
Beispieldokument
Hier nun ein minimalistisches Beispiel mit den Informationen, welche wir bisher gelernt haben.
\documentclass[a4paper,10pt]{article}
\usepackage[ngerman]{babel}
\begin{document}
Das ist ein Dokument.
\end{document}
Ergebnis Beispieldokument
Ich möchte an dieser Stelle kurz zeigen, wie das hier genannte Beispiel nach dem Kompilieren aussehen würde. Wie der Kompiliervorgang funktioniert etc., wird später erklärt.
Weg eines LaTeX Dokumentes
Bevor wir das erste mal unser LaTeX Dokument kompilieren, welches wir geschrieben haben (unser minimales Beispiel: 10.1.3), sollten wir uns kurz Gedanken machen, was mit unserem LaTeX Dokument alles passiert. Welche Wege es geht bzw. gehen kann.
Erstellen
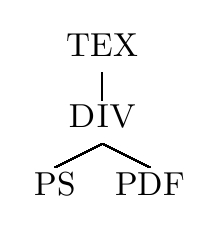
Wir erstellen mit unserem Lieblingseditor (z.B. Kate) unser Dokument und speichern dieses als *.tex Datei ab. Die Dateiendung .*tex steht, wie nicht anders zu erwarten, für LaTeX bzw. TeX. Dieses *.tex File beinhaltet unseren LaTeX Quellcode, welcher kompiliert werden muss, um das Ergebnis ansehen zu können. Nach dem Kompilieren, erhalten wir div. Dateien. Unter diesen Dateien finden wir unseren gewünschten Text i.d.r als Datei im DVI - Device independent file format.
Weiterverarbeiten
Nach dem erstellen einer Datei im DVI - Device independent file format kann diese dann beispielsweise in das PS - PostScript oder das PDF - Portable Document Format weiterverarbeitet werden.
Dateiendungen
Hier möchte ich schnell die Dateiendungen nennen, welche uns beim Arbeiten mit LaTeX unter die Augen kommen.
.tex
Ist die Eingabedatei, welche mit Hilfe eines Editors erstellt und im ASCII Format gespeichert wird.
.dvi
Die Datei enthält nach dem Kompilieren den druckfertigen Text.
.log
Die Logdateien enthalten alle Fehlermeldungen, die beim Kompilierdurchgang erzeugt wurden.
.aux
Enthält Verzeichnisse und Verweise.
.toc
Diese Datei enthält das Inhaltsverzeichnis eines Dokumentes, sofern eines im Dokument vorhanden bzw. angelegt wurde.
.sty
Style Datei, welche von LaTeX bereitgestellt wird oder von einem selbst hinzugefügt wurde.
.bbl
Enthält die Literatur eines Dokumentes und wird von BibTeX erzeugt.
.bib
BibTeX Eingabedatei, welche eine Literaturdatenbank enthält.
.lof, .lot, .idy
Diese Dateien enthalten weitere Listen und Verweise.
Kompilieren
Nun ist es soweit. Wir werden unseren Quelltext kompilieren. Alles was man hierzu braucht ist der Quelltext in abgespeicherter Form als *.tex Datei und eine Konsole bzw. ein Terminal. Die Eingabe schaut dann wie folgt aus:
Kompilieren in DVI
:~> latex beispiel.tex
Mit diesem Befehl, sollte die Datei beispiel.tex, welche den Quelltext enthält, kompiliert werden. Als Ergebnis erhalten wird eine beispiel.dvi Datei. Zur Veranschaulichung hier ein Konsolenfenster beim Kompilieren:
Kompilieren in PDF
Es ist problemlos möglich aus seinem Quellcode eine PDF zu erzeugen, hierzu wieder eine Konsole mit folgendem Befehl:
:~> pdflatex beispiel.tex
Wir sollten nach ein paar Sekunden kompilieren eine PDF Datei erhalten, wie auch eine *.aux und *.log Datei.
Umwandeln in PostScript
Um eine PostScript Datei zu erzeugen muss das DVI File in diese umgewandelt werden, was folgendermaßen funktioniert.
:~> dvips beispiel.dvi
Würde aus unserer DVI Datei eine PostScript Datei erzeugen.
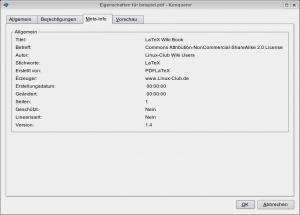
PDF Meta Informationen
Sollte man vorhaben, den LaTeX Quellcode in eine PDF Datei zu kompilieren, so besteht die Möglichkeit diverse Meta-Informationen der Datei mit zu geben.
Zu den Meta Informationen gehören zum Beispiel:
- Title
- Creator
- Producer
- Author
- CreationDate
- ModDate
- Subject
- Keywords
Im Quellcode kann dies dann so aussehen:
\begin{document}
\pdfinfo {
/Title (LaTeX Wiki Book)
/Creator (PDFLaTeX)
/Producer (www.Linux-Club.de)
/Author (Linux-Club Wiki Users)
/CreationDate (x)
/ModDate (x)
/Subject (Commons Attribution-NonCommercial-ShareAlike 2.0 License)
/Keywords (LaTeX)
}
Dieses Dokument enthält von mir festgelegte Meta Informationen.
\end{document}
Betrachter
Nach dem Kompiliervorgang kann unser fertiges Dokument betrachtet werden. Je nach Dateiformat ist hier der entsprechende Betrachter zu verwenden.
- DVI - Hier eignet sich unter KDE das Werkzeug KDVI.
- PDF - Entweder den KDE eigenen KPDF oder den Acrobat Reader von Adobe, welchen es auch für Linux gibt.
- PS - Hier kann unter KDE ebenfalls KPDF verwendet werden.
Natürlich gibt es noch weitere Betrachtungswerkzeuge. Ich selbst habe mich hier nur auf diejenigen Betrachter bezogen, welche ich persönlich kenne und als KDE Nutzer verwende.
Schnellkurs mit Kile
Der erste Start
Das folgende Bild zeigt Kile für OpenSuse 10.2 von Packman nach dem ersten Start.
Das erste Beispieldokument aus dem Schnellkurs
Wir wollen das erste Beispieldokument aus dem Schnellkurs mit Kile setzen. Dazu wählen wir in Datei => Neu. Nun erscheint eine Auswahlbox. Wir wählen erstmal "Empty Dokument" und klicken auf OK. Jetzt erscheint erneut eine Auswahlbox. Sie ist sehr interessant! Wir klicken trotzdem auf Abbrechen. Jetzt könnten wir den Code aus dem ersten Beispieldokument in das leere Fenster kopieren. Hier ist er noch einmal:
\documentclass[a4paper,10pt]{article}
\usepackage[ngerman]{babel}
\begin{document}
Das ist ein Dokument.
\end{document}
Wir werden aber ausnahmsweise mal tippen. Bereits nach den ersten 3 Zeichen \do öffnet sich eine Auswahlbox. Kile bietet hier an, den Code zu vervollständigen. Wir nehmen dieses Angebot natürlich an.
Fertig? Dann können wir das Dokument speichern und kompilieren. Unter "Datei" finden wir die üblichen Öffnen und Speichern Dialoge. Sehr interessant ist der Eintrag "Vorlage aus Dokument erzeugen". Dazu später. Wir speichern nun unter dem Namen "Beispiel.tex".
Wir klicken auf "Erstellen" => Kompilieren. Dort finden wir eine Reihe von Einträgen. Hier ist der Eintrag LaTeX wichtig. (Eventuell noch PDFLaTeX). Wir klicken zweimal auf "LaTeX". Nach dem ersten Klick erscheint eine Warnung. Diese ist nach dem zweiten Klick auf LaTeX verschwunden.
Und damit sind wir auch schon fertig! Wir wollen jetzt unser Werk betrachten. Das können wir auch von Kile. Dazu klicken wir auf "Erstellen" => Ansicht => ViewDVI.
What you see is what you get
Wir erhalten auf jeden Fall, was wir im DVI-Betrachter sehen!
Wir lassen erstmal den DVI-Betrachter und Kile geöffnet. Nun schreiben wir noch folgenden Satz in unser Beispiel: Das macht ja Spass.
\documentclass[a4paper,10pt]{article}
\usepackage[ngerman]{babel}
\begin{document}
Das ist ein Dokument. Das macht ja Spass.
\end{document}
Nun klicken wir erneut auf "LaTeX" und schauen auf den DVI-Betrachter. Wie von Geisterhand erscheint der Satz auch hier. Das funktioniert allerdings nur, wenn der DVI-Betrachter von Kile aus gestartet wurde. So wie im DVI-Betrachter dargestellt, wird auch das Druckergebnis aussehen.
So sieht das jetzt aus. Wir können jetzt weiter an unserem Dokument schreiben. Ein einziger Klick auf den Knopf "LaTeX" macht die Änderungen auch im DVI-Betrachter sichtbar.
Grundlagen Teil 1
Nachdem wir nun in der Lage sind, ein einfaches Dokument in LaTeX zu schreiben, zu kompilieren und das Ergebnis begutachten zu können sowie zu drucken etc., wird es nun Zeit, ein paar Grundlagen zu erlernen. Das reine Schreiben eines Textes reicht bei weitem nicht aus, um die alltäglich anfallenden Aufgaben mit LaTeX erledigen zu können. Im weiteren Verlauf wird auf die wichtigsten Befehle eingegangen, welche benötigt werden, um unser bereits genanntes Ziel im Einleitungsbereich erreichen zu können.
Seitenränder
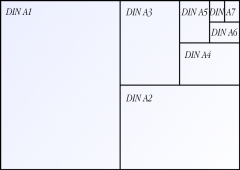
Seitenränder werden in unserem Dokument mit in der Präambel eingestellt. Ich möchte hier im Beispiel eines normalen DIN A4 Blattes mit von mir angegebenen Größen für die Ränder zeigen.
\usepackage[a4paper,
left=1.8cm, right=2.0cm,
top=1.1cm, bottom=2.2cm]{geometry}
Wie im Beispiel zu sehen ist, werden die Zahlenwerte in der Maßeinheit cm angegeben. Als Beispielpapier wurde von mir ein DIN A4 Blatt verwendet, was aber auch durch z.B. ein DIN A5 getauscht werden kann. Als Paket laden wir hier {geometry}.
Rechtschreibung
Es ist sinnvoll, mit anzugeben, welche Rechtschreibung wir nutzen möchten. Dies sollte bitte nicht mit einer Rechtschreibkorrektur verwechselt werden!
Möglichkeiten, welche wir hier wählen können, sind zum Beispiel:
- ngerman
- german
- french
- dutch
\usepackage[ngerman]{babel}
Hier ist also das Ergänzungspaket babel mit der Option ngerman.
ngerman
Mit ngerman erhalten wir hier die neue deutsche Rechtschreibung, was bedeutet, dass das LaTeX unsere Silben falls nötig nach den reformierten Regeln trennt.
P.S. Als wirklich neue deutsche Rechtschreibung kann man ngerman nicht sehen, wenn man sich anschaut, wie oft sich in unserer Rechtschreibung etwas ändert.
Zeichensatzkodierung
Es gibt mittlerweile recht viele verschiedene Zeichensätze. Man sollte sich also Gedanken machen, in welchem Zeichensatz man sein Dokument erstellen möchte.
In unserer Präambel hat dies dann so auszusehen:
\usepackage[utf8]{inputenc}
Hier wurde von mir der Zeichensatz utf8 gewählt. Umlaute wie ä,ö,ü konnen hierdurch ganz normal geschrieben werden und müssen nicht wie bei latin9 unter LaTeX als "a, "o, "u geschrieben werden.
latin9
ISO 8859-15 / IEC 8859-15 ist ein von der Internationalen Organisation für Normungen zuletzt 1999 aktualisierter Standard für die Informationstechnik zur Zeichenkodierung mit acht Bit. Die ISO 8859-15 versucht sehr viele Sonderzeichen aus dem westeuropäischen Raum abzudecken.
utf-8
Das 8-bit Unicode Transformation Format, ist die wohl am weitesten verbreitete Kodierung für Unicode Zeichen. Sie bietet die meisten alphabethischen Schriftzeichensysteme, welche überhaupt genutzt werden können. Dies sind lateinische Buchstaben, arabische Zahlen, griechische, koreanische wie auch thailändische Schriften. UTF-8 ist von der Internet Engineering Task Force dem Unicode Consortium und von der Internationalen Organisation für Normungen identisch definiert in den Normdokumenten RFC 3629 / SD 63 (2003) ISO 10646.
Teildokumente
Sollte einmal ein etwas groeßeres Dokument verfasst werden, welches mehrere große Teile hat, so kann es vorteilhaft sein, diese einzelnen Teile oder Kapitel auch in einzelnen Dateien zu speichern und sie dann in das Hauptdokument einzubinden. Dies funktioniert ganz einfach. Man schreibt seinen gewünschten Text in seinem Dokument und setzt an die Stelle, an der der Text eines weiteren Dokumentes eingefügt werden soll, folgenden Befehl:
\input{blumen.tex}
In diesem Beispiel würde nun der Text der Datei blumen.tex eingefügt werden. Wichtig bei der ganzen Geschichte ist, dass die Datei blumen.tex in diesem Fall keine Präambel hat. Genauso darf sie kein /begin{document} und /end{document} beinhalten. Einfach nur den reinen Text mit den entsprechenden Befehlen für die Formatierung des Textes.
\input{..}
ist also der entsprechende Befehl, welcher zu verwenden ist. Der Grund weshalb ich den Punkt Teildokumente recht weit an den Anfang der Grundlagen setzte, ist der, dass man sich bereits im Vorfeld Gedanken darüber macht, wie groß das Dokument u.U. wird, um später nicht in einer *.tex Quelldatei Datei zu landen mit über 10.000 Zeilen wenn es denn auch einfacher geht, die einzelnen Kapitel etc. zu verwalten und zu bearbeiten.
Absatz
Es gibt zwei Möglichkeiten einen Absatz zu erzeugen. Entweder verwenden wir den Befehl:
\par
Oder wir fügen eine Leerzeile ein. Hier beide Beispiele:
\begin{document}
Dies ist der eigentliche Text \par in unserem Dokument.
\end{document}
oder
\begin{document}
Dies ist der eigentliche Text
in unserem Dokument.
\end{document}
Beide Formen würden am Ende das selbe Ergebnis bringen und in unserem fertigen Dokument so aussehen:
Eingerückter Absatz
Ob der Absatz eingerückt wird oder nicht, ist von der jeweiligen Dokumentenklasse abhängig.
Mit dem Befehl \noindent kann man dem Einrücken entgegenwirken.
\noindent
Ein Beispiel möchte ich hier zeigen:
\begin{document}
Dies ist der eigentliche Text ohne noindent in unserem Dokument. Deshalb sollte hier die erste Zeile eingerückt werden.
\end{document}
\begin{document}
\noindent
Dies ist der eigentliche Text mit noindent in unserem Dokument. Deshalb sollte hier keine Zeile eingerückt werden.
\end{document}
Eine weitere Form wäre die dauerhafte Unterdrückung:
\parindent0pt
Durch die zusätzliche Angabe von 0pt, was für null Punkte steht, werden alle nachfolgenden Absätze um Null Punkte eingerückt. D.h. es gibt keine weiteren Einrückungen bei den Absätzen.
Diese Art der Unterdrückung kann auch entsprechend den eigenen Wünschen angepasst werden. So ist es z.B. durch die Angabe der Anzahl der Punkte möglich, die Weite der Einrückung zu bestimmen.
Beispiel:
\begin{document}
\parindent50pt
In diesem hier erstellten Text sollte der Absatz durch die Angabe von 50pt um 50 Punkte eingerückt werden.
\end{document}
Weshalb werden Absätze eigentlich eingerückt?
Schreib man einen Text in Blocksatz, so läuft in der Regel die letzte Zeile von ihrer Länge her einfach aus. Sollte diese aber durch einen Zufall genauso lang sein, wie die Zeilen des Blocksatzes, so würde man einen neu beginnenden Textabschnitt ebenfalls im Blocksatz ( z.B. beim schreiben eines Buches ) nur sehr schlecht als solchen erkennen. Die Einrückungen neuer Absätze erleichtern daher die Lesbarkeit des Textes, da neue Absätze sehr leicht als solche zu erkennen sind.
Zeilenumbruch
Im Normalfall sorgt LaTeX automatisch für den Zeilenumbruch. D.h. wir können in unserer Quelldatei alles hintereinander in eine Zeile schreiben. Wem dieses Vorgehen nicht gefallen sollte und wer LaTeX zu einem Umbruch zwingen will, der kann dies mit zwei \\ tun.
\\
Beispiel ohne den erzwungenen Zeilenumbruch:
\begin{document}
\noindent
Ich moechte hier und hier und auch hier einen Zeilenumbruch haben um euch diese tolle Funktion zeigen zu koennen.
\end{document}
Nun das selbe mit einem von mir erzwungenem Zeilenumbruch:
\begin{document}
\noindent
Ich moechte hier \\ und hier \\ und auch hier \\ einen Zeilenumbruch haben, \\ um euch diese tolle
Funktion \\ zeigen zu können.
\end{document}
Größe des Zeilenumbruchs
Wer einen gewissen Abstand zwischen einem Zeilenumbruch angeben möchte kann dies auf einfache Art und Weise tun.
Beispiel mit Angabe in der Maßeinheit cm:
\begin{document}
\noindent
Hier ist ein Text \\
den ich geschrieben habe \\[0.8cm]
mit einem Zeilenumbruch \\
von ca. 0.8cm. \\
\end{document}
Umlaute
Wie schreibe ich Umlaute, um mir das lästige ae, oe und ue zu ersparen ?
Beispiel:
\begin{document}
"a, "A, "o, "O, "u, "U, "s
\end{document}
Die Ausgabe sähe dann so aus:
Eine weitere Möglichkeit wäre die Verwendung des utf8 Zeichensatzes bei dem die Umlaute ganz normal geschrieben werden können was bei latin9 nicht der Fall ist.
Akzente
Das schreiben von Akzenten wird ebenfalls ab und an mal gebraucht, meist wenn man irgendwelche Namen von Personen zu schreiben hat.
\begin{document}
\^{a} \`{a} \'{a} \c{c} \~{a} \"\i{} \o
\end{document}
Würde wie folgt im späteren Dokument aussehen:
Dies sind mit Sicherheit nicht alle, aber es sind wohl die am meist verwendeten.
Textgestaltung
Kein Text sollte einfach nur niedergeschrieben bzw. runtergeschrieben werden, ohne dass sich der Autor ein paar Gedanken über den Aufbau macht.
Textabschnitte
Unter LaTeX ist es sehr einfach, einen Textabschnitt mit einer bestimmten Ebene zu erstellen. Beim Erzeugen eines solchen Textabschnittes wird die zugehörige Überschrift erstellt, wie auch einen Eintrag in das Inhaltsverzeichnis des Dokumentes (falls vorhanden) vorgenommen.
- Part
- Chapter
- Section
- SubSection
- SubSubSection
- Paragraph
- SubParagraph
Die hier aufgelisteten Gliederungen beginnen bei Part der höchsten Gliederungsebene und endet bei SubParagraph der untersten Gliederungsebene.
Die zweithöchste Ebene Chapter gibt es allerdings nur bei der Verwendung der Dokumentenklassen Book und Report.
Part
Einen Part verwendet man in der Regel nur bei sehr großen Dokumenten. Part 1 und Part 2 wären in etwa so wie wenn man ein Buch oder einen Roman liest, der aus mehreren Teilen besteht.
In der alltäglichen Arbeit verwendet man normalerweise als höchsten Abschnitt die Section. Dennoch möchte ich hier ein kleines Beispiel für einen Part zeigen.
\begin{document}
\part{Der erste Tag}
Dies ist der erste Tag.
\part{Der zweite Tag}
Und dies der zweite.
\end{document}
Wie hier im Beispiel des Quelltextes zu sehen ist, erstellen wir einen Teil mit dem Titel "Der erste Tag" und einen weiteren Teil mit dem Titel "Der zweite Tag".
Darunter steht dann der jeweilige Text für den entsprechenden Teil.
Chapter
Wie bereits erwähnt, kommt Chapter nur in Book oder Report zum Einsatz. Es ist eine Art Zwischenstufe von Part und Section.
\begin{document}
\chapter{Der erste Tag}
Heute beginnt der erste Tag.
\end{document}
Section
Eine Section ist im Normalfall die Ebene welche man als höchste in seinen alltäglichen Dokumenten verwendet. Hier ein einfaches Beispiel:
\begin{document}
\section{Textformate}
Hier die wohl bekanntesten Formate: TEX, TEXT
\section{Audioformate}
Diese kennt jeder: MP3, OGG
\section{Videoformate}
Und hier noch ein paar: VOB, DIVX
\end{document}
In diesem Beispiel sind 3 verschiedene Sectionen zu sehen. Textformate, Audioformate und Videoformate.
SubSection
Wie bei der Section hier ein weiteres Beispiel mit drei SubSectionen in einem Dokument.
\begin{document}
\subsection{Textformate}
Hier die wohl bekanntesten Formate: TEX, TEXT
\subsection{Audioformate}
Diese kennt jeder: MP3, OGG
\subsection{Videoformate}
Und hier noch ein paar: VOB, DIVX
\end{document}
Auffällig und gut zu sehen ist hier die Nummerierung vor den Überschriften. Es ist klar zu erkennen, dass eine Section eine höhere Zahl (Zahl 1) in oberem Beispiel hat als eine SubSection (Zahl 0.1) in diesem Beispiel.
SubSubSection
Wie bei der SubSection so ist auch hier die niedrigere Zahl ( 0.0.1 ) zu erkennen.
\begin{document}
\subsubsection{Textformate}
Hier die wohl bekanntesten Formate: TEX, TEXT
\subsubsection{Audioformate}
Diese kennt jeder: MP3, OGG
\subsubsection{Videoformate}
Und hier noch ein paar: VOB, DIVX
\end{document}
Paragraph
Der Paragraph befindet sich bereits auf einer so tiefen Ebene, das hier keine Zahlenwerte mehr angegeben werden. Wie unschwer zu erkennen, werden tiefere Ebenen mit einer kleineren Schrift und höhere mit einer größeren Schrift dargestellt.
\begin{document}
\paragraph{Textformate}
Hier die wohl bekanntesten Formate: TEX, TEXT
\paragraph{Audioformate}
Diese kennt jeder: MP3, OGG
\paragraph{Videoformate}
Und hier noch ein paar: VOB, DIVX
\end{document}
SubParagraph
Die tiefste Ebene überhaupt stellt der SubParagraph dar.
\begin{document}
\subparagraph{Textformate}
Hier die wohl bekanntesten Formate: TEX, TEXT
\subparagraph{Audioformate}
Diese kennt jeder: MP3, OGG
\subparagraph{Videoformate}
Und hier noch ein paar: VOB, DIVX
\end{document}
Textabschnitt - Beispiel
Hier möchte ich ein weiteres Beispiel von der Section bis zum SubParagraphen plus eines Inhaltverzeichnisses zeigen.
\begin{document}
\tableofcontents
\section{Petabyte}
Sehr gross, hier werden wir hoffendlich bald sein.
\subsection{Terabyte}
Gross, da kommen wir bald hin.
\subsubsection{Gigabyte}
Normal, hier sind wir heute.
\paragraph{Megabyte}
Klein, aber bereits besser.
\subparagraph{Kilobyte}
Sehr klein, so hatte alles angefangen. \\
\end{document}
Überschriften im Textabschnitt
Bei der Angabe der Textabschnitte wie Section, SubSection etc. haben wir die Möglichkeit, unsere Überschrift als normalen Text oder Kurzform anzugeben.
Syntax bei Section:
\section[Kurzform]{Überschrift}
Seither haben wir in den bisherigen Beispielen immer eine Überschrift in den geschweiften Klammern angegeben. Sollte man in seinem Dokument ein Inhaltsverzeichnis aufbauen, so hat man die Möglichkeit, mit der [Kurzform] eine andere Beschreibung im Inhaltsverzeichnis zu verwenden, als der Name der Überschrift, welcher im Normalfall dorthin mit übernommen wird. Zum besseren Verständnis folgt ein kleines Beispiel:
\begin{document}
\tableofcontents
\subsection[Masseinheit]{Petabyte}
Sehr gross, hier werden wir hoffendlich bald sein.
\end{document}
Nummerierung
Wem die Nummerierung beim Erstellen der einzelnen Textabschnitte nicht gefällt, kann diese auch unterdrücken, was allerdings zudem den Effekt hat, dass dieser Textabschnitt nicht mehr im Inhaltsverzeichnis (wenn vorhanden) gelistet wird.
Die Unterdrückung funktioniert mit einem Sternchen * wie im Beispiel zu sehen.
\begin{document}
\tableofcontents
\subsection*{Petabyte}
Sehr groß, hier werden wir hoffendlich bald sein.
\end{document}
Zum Vergleich ohne die Unterdrückung.
\begin{document}
\tableofcontents
\subsection{Petabyte}
Sehr groß, hier werden wir hoffendlich bald sein.
\end{document}
Es ist desweiteren möglich die Überschriften ohne ihre Nummerierung so darzustellen, das sie bei der Verwendung eines Inhaltsverzeichnisses dennoch mit der dazu passenden Seite gelistet werden. Um dies erreichen zu können, ist der Befehl: \setcounter{secnumdepth}{-1} einzufügen wie im Beispiel zu sehen.
\begin{document}
\tableofcontents
\setcounter{secnumdepth}{-1}
\subsection{Subsection}
SubSection Überschrieft ohne Nummer und mit Seitenzahl Eintrag ins Inhaltsverzeichniss.
\end{document}
Inhaltsverzeichniss
Da wir in den letzten Beispielen bereits ein Paar mal über das Wort Inhaltsverzeichnis gestolpert sind, möchte ich schnell die Syntax hierfür zeigen.
Ein Inhaltsverzeichnis kann mit dem Befehl:
\tableofcontents
erstellt werden. Alle Textabschnitte, welche nicht unterdrückt wurden, werden in der Regel hier automatisch aufgelistet und durchnummeriert. Es kann gut möglich sein, dass nach dem ersten Durchgang beim Kompilieren das Inhaltsverzeichnis nicht ganz so ist, wie es sein sollte. D.h. nach einer Änderung, z.B. einem weiteren hinzugefügtem SubSection, ist dieser Eintrag noch nicht vorhanden oder die angegebene Seitenzahl stimmt nicht. Sollte dies der Fall sein, muss man LaTeX einfach ein zweites mal durchlaufen lassen, da beim ersten Durchlauf das Inhaltsverzeichnis erzeugt aber noch nicht in die Datei geschrieben wird.
Text Typografie
Auf die üblichen Gestaltungsoptionen, welche einem beim Erstellen von Texten zur Verfügung stehen, muss auch unter LaTeX nicht verzichten werden.
- Blocksatz
- Mittelachsensatz
- Linksbündiger Flattersatz
- Rechtsbündiger Flattersatz
Blocksatz
Über den Blocksatz müssen wir uns keine großen Gedanken machen, da dieser default ist. Blocksatz heißt, dass der Text links wie auch rechts gleichbündig gesetzt oder auf gleiche Länge gebracht wird. Der letzte Absatz im Blocksatz, orientiert sich meist am linken Rand und läuft dann von seiner Länge her einfach aus.
Verwendet wird der Blocksatz meist bei:
- Büchern
- Illustrierten
- Zeitungen
Beispiel:
\begin{document}
Dieser von mir geschriebener Text sollte in unserem fertigen Dokument als Text im Blocksatz dargestellt werden. Blocksatz bedeutet,
dass der Text links wie auch rechts gleichbündig gesetzt oder auf gleiche Länge gebracht wird. Der letzte Absatz im Blocksatz, orientiert
sich meist am linken Rand und läuft dann von seiner Länge her einfach aus.
\end{document}
Mittelachsensatz
Mittelachsensatz, auch als axialer, symmetrischer oder zentrierter Satz bekannt, wird meist bei
- Gedichte
- Titelblätter
- Urkunden
verwendet. Zum Schreiben größerer Texte ist er eher ungeeignet.
Beispiel:
\begin{document}
Hier die erste Zeile, welche default im Blocksatz geschrieben wird, gefolgt von einer weiteren welche Zentriert wurde.
\begin{center}
Dies ist nun die Zentrierte Zeile.
\end{center}
Und nun geht es wieder ganz normal im Blocksatz weiter, wie schon im oberen Teil mit der ersten eingerückten Zeile.
\end{document}
Linksbündiger Flattersatz
Findet Verwendung und eignet sich bei:
- Gedichten
- Kurzen texten
- Anzeigen
Beispiel:
\begin{document}
\begin{flushleft}
Dies ist ein Text, welchen ich zur Demonstration hier im Beispiel als linksbuendigen Text formatiere. Unschwer zu erkennen ist der Flatterrand auf der rechten Seite.
\end{flushleft}
\end{document}
Rechtsbündiger Flattersatz
Beim Rechtsbündigen Flattersatz ist es genau andersherum wie beim linksbündigen Flattersatz.
Verwendung:
- Werbung
- Bildunterschriften
Beispiel:
\begin{document}
\begin{flushright}
Dies ist ein Text, welchen ich zur Demonstration hier im Beispiel als rechtsbuendigen Text formatiere. Unschwer zu erkennen ist der Flatterrand auf der linken Seite.
\end{flushright}
\end{document}
Schriftauszeichnung
Ganze Texte oder einzelne Teile - natürlich auch nur Wörter - können auf unterschiedliche Art und Weise hervorgehoben werden. Ich möchte hier schnell die Bekanntesten zeigen.
Fett
Diese Option dient in der Regel dazu, um einzelne wichtige Wörter eines Textes hervorzuheben.
\begin{document}
Ein normaler nicht fetter Text.
\textbf{Alles was in den geschweiften Klammern steht, ist fett.}
Und wieder ein normaler nicht fetter Text.
\end{document}
Geneigt
Eine geneigte oder Schräge Schrift ist zwar geneigt, allerdings nicht so sehr wie eine kursive Schrift.
\begin{document}
Ein normaler Text.
\textsl{Alles was in den geschweiften Klammern steht, ist etwas schräg.}
Und wieder ein normaler Text.
\end{document}
Kursiv
Zum Einsatz kommen sollte eine kursive Schrift immer dann, wenn man eine bestimmte Stelle im Text hervorheben möchte, wie beispielsweise Zitate.
\begin{document}
Ein normaler Text.
\textit{Alles was in den geschweiften Klammern steht, ist kursiv.}
Und wieder ein normaler Text.
\end{document}
Anstelle von
\textit{..}
kann auch
\emph{..}
verwendet werden, das Ergebnis ist das selbige.
Unterstrichen
Das unterstreichen sollte nur dann gewählt werden, wenn keine anderen Auszeichnungsmöglichkeiten genommen werden können.
\begin{document}
\underline{Alles was in den geschweiften Klammern steht, ist unterstrichen.}
\end{document}
Aufrechte Schrift
Im Mathematischen Formelsatz wird kursiv für Variablen und aufrecht für Funktionsnamen verwendet.
\begin{document}
\textup{Alles was in den geschweiften Klammern steht, ist aufrecht.}
\end{document}
Keine Interpretation
Man hat die Möglichkeit, einen Text mit eventuell auch LaTeX Befehlen schreiben zu können, ohne dass diese von LaTeX interpretiert werden.
\begin{document}
\verb|Dies kann man auch einen eingebetteten Programmcode nennen.|
\end{document}
Anstelle von
\verb|..|
kann man auch
\texttt{..}
verwenden.
Sperren
Für das sperren von Wörtern oder Buchstaben kann das Paket soul verwendet werden. Zum laden dies in die Präambel eintragen:
\usepackage{soul}
Gesperrt wird in der Regel nur sehr selten. Die Kleinbuchstaben ( Minuskeln ) sollte man auf keinen Fall sperren. Wenn überhaupt gesperrt werden darf, dann wäre dies höchstens bei der Verwendung eines Wortes das in reinen Großbuchstaben ( Versalien ) geschrieben ist. Aussehen könnte dies dann in etwa so wie im Beispiel zu sehen.
Das ist ein \so{GESPERRTES} Wort im Text
Textschriften
Wie bei vielen anderen Officeprogrammen, so hat man auch unter LaTeX die Wahl der entsprechenden Textschrift.
Roman
Die Roman Textschrift, welche uns unter LaTeX zu Verfügung steht, ist eine Schrift der Computer Modern Roman Schriftfamilie.
Diese Schriftsippe Computer Modern wurde von Donald E. Knuth für sein TeX entwickelt und ist in Metafont geschrieben.
Roman ist eine proportionale Textschrift, welche Serifen enthält. Serifen sind sehr kleine feine Linien, die einen Buchstabenstrich am Ende zu seiner Grundlinie abschließen. Längere Texte werden i.d.R. in einer solchen Textschrift mit Serifen gedruckt, da man durch die Serifen eine bessere Lesbarkeit erreicht.
\begin{document}
\rmfamily{Das ist eine Serifenschrift namens Roman.}
\end{document}
SansSerif
Die genaue Bezeichnung ist hier: Computer Modern SansSerif
Sie wurde von Richard Southall entwickelt und ist eine auf den Formen der Roman basierenden serifenlose Schrift. Serifen sind sehr kleine feine Linien die einen Buchstabenstrich am Ende zu seiner Grundlinie abschließen. Schriften ohne Serifen wurden meist für kurze Texte oder Übersdchrifften verwendet, in der heutigen Zeit soll sie ausschliesslich als Brotschrift verwendet werden, jedenfalls wenn es nach den Grossen Meistern der Typografie wie beispielsweisse Jan Tschichold geht. Letztenendes muss allerdings der Gestallter wissen welche Schrift die beste für sein Text ist.
\begin{document}
\sffamily{Das ist eine serifenlose Schrift namens Sansserif.}
\end{document}
Monospace
Hier lautet die genaue Bezeichnung Computer Modern Typewriter, welche eine in der Form zu Roman passende Schreibmaschinen-Schrift ist.
\begin{document}
\ttfamily{Die Monospace Schrift, aehnlich einer Schreibmaschienen Schrift.}
\end{document}
Kapitälchen
Bei Kapitälchen werden alle Kleinbuchstaben groß geschrieben und dennoch sind sie kleiner als die Großbuchstaben. Ihre Strichstärke und die Grauwerte orientieren sich an der Computer Modern Gemeinde wie auch an der Roman Textschrift.
Verwendung findet Kapitälchen aktuell meist nur bei Namen oder den ersten Buchstaben bei einem neuen Absatz. In der deutschen Ligatur gilt hier übrigens das ein ß durch zwei ss dargestellt wird.
\begin{document}
\textsc{Das ist Kapitaelchen.}
\end{document}
Was sind Serifen
Hier ein Beispiel in dem man die Serifen, welche leicht rot eingefärbt wurden, recht gut erkennen kann.
Farben
Schriftfarben sind ein wichtiger Bestandteil der Auszeichnungsarten. So können wichtige Wörter eines Textes mit einer roten Farbe hervorgehoben werden.
Wie man Farben unter LaTeX verwenden kann, möchte ich hier schnell demonstrieren.
Bevor wir Farbe in unserem Dokument verwenden können, muss ein weiteres Paket namens color geladen werden. Um dies zu tun, ist folgende Zeile in die Präambel mit aufzunehmen:
\usepackage{color}
Nun haben wir die Möglichkeit unseren Text, welchen wir verfassen, wie auch dessen Hintergrund farblich zu gestalten.
Schriftfarbe
Ein kleines Beispiel für einen farbigen Text.
\begin{document}
\textcolor{blue}{Dieser Text waere in der Farbe Blau.}
\end{document}
Wie unschwer zu erkennen ist, kann mit der Angabe in den geschweiften Klammern die Textfarbe bestimmt werden. Weitere Möglichkeiten wären:
- blue
- black
- green
- red
- yellow
- cyan
- magenta
- white
Hinweis: Der folgende Code funktioniert offenbar nicht im DVI-Betrachter.
\begin{document}
\textcolor{yellow}{Dieser Text waere in der Farbe gelb.}
\end{document}
Die Farbe gelb wird aber im Postscriptdokument und auch im PDF richtig angezeigt. Wenn man die Farbe gelb auch im DVI-Betrachter sehen will, dann kann man folgenden Code verwenden:
\begin{document}
\textcolor{rgb:yellow,1}{Dieser Text waere in der Farbe Gelb.}
\end{document}
Hierfür muss dann in der Präambel anstelle des Paketes color das Paket xcolor eingebunden werden.
\usepackage{xcolor}
Seitenfarbe
So wie die Farbe des Textes gewählt werden kann, funktioniert es auch bei der Farbe für die Seite selbst.
\pagecolor{blue}
Würde die Blattfarbe in blau einfärben. Wichtig hierbei ist, dass auch alle nachfolgenden Seiten blau sind. Möchte man beispielsweise nach drei blauen Seiten wieder eine weiße Seite haben, so muss dies angegeben werden.
\pagecolor{white}
Mögliche Farben sind:
- blue
- black
- green
- red
- yellow
- cyan
- magenta
- white
Beispiel:
\begin{document}
\pagecolor{black}
\textcolor{white}{Ein schwarzer Hintergrund.}
\end{document}
Schriftmasse
Als Schriftmaß wird die Schriftgröße oder auch der Schriftgrad bezeichnet, welcher mit einem Typometer gemessen wird. Zum Messen selbst wird hier die so genannte Kegelhöhe verwendet und nicht, wie von vielen angenommen, die Versalhöhe. Derzeit ist dies in der DIN 16507-1 vom September 1998 so festgeschrieben. Man arbeitet im Moment an einer neuen DIN 16-507-2 bei welcher nicht mehr die Kegelhöhe, sondern die Versalhöhe zum bestimmen der richtigen Größe genommen werden soll. Wann genau und ob sich dies überhaupt durchsetzten wird, ist abzuwarten.
Möglich sind:
- tiny
- scriptsize
- footnotesize
- small
- normalsize
- large
- Large
- LARGE
- huge
- HUGE
Hier ist es wichtig, auf die korrekte Schreibweise (gross/klein) zu achten. Es macht einen enormen Unterschied zwischen large, Large oder LARGE.
Winzig klein
\begin{document}
\begin{tiny}Das ist winzig klein\end{tiny}
\end{document}
Sehr klein
\begin{document}
\begin{scriptsize}Das ist sehr klein.\end{scriptsize}
\end{document}
Kleiner
\begin{document}
\begin{footnotesize}Das ist eine Mischung aus sehr klein und winzig klein.\end{footnotesize}
\end{document}
Klein
\begin{document}
\begin{small}Das ist eine kleine Schriftgroesse.\end{small}
\end{document}
Normal
begin{document}
\begin{normalsize}Das ist die normale Schriftgroesse.\end{normalsize}
\end{document}
Groß
\begin{document}
\begin{large}Das ist eine grosse Schriftgröße.\end{large}
\end{document}
Größer
\begin{document}
\begin{Large}Das ist eine größere Schriftgröße.\end{Large}
\end{document}
Sehr groß
\begin{document}
\begin{LARGE}Das ist eine sehr grosse Schriftgroesse.\end{LARGE}
\end{document}
Riesig groß
\begin{document}
\begin{huge}Das ist eine riesig große Schriftgröße.\end{huge}
\end{document}
Gigantisch
\begin{document}
\begin{Huge}Das ist eine gigantisch große Schriftgröße.\end{Huge}
\end{document}
Und noch viel größer
Mit dem Befehl \scalebox{Faktor}{Text} kann man Text beliebig groß setzen. Man wird nur durch die Größe des Papieres beschränkt. Im folgenden Beispiel vergrößern wir ein f um den Faktor 78:
Beispiel: (Auf PDF eingestellt)
\documentclass[a4paper]{article}
%\usepackage[dvips]{graphicx}
\usepackage[pdftex]{graphicx}
\begin{document}
\scalebox{78}{f}
\end{document}
Hinweis 1: Dieses Beispiel funktioniert mit pdflatex. Im fertigen PDF sieht man ein f, welches das ganze Blatt ausfüllt. ( Der Befehl pdflatex muß zweimal ausgeführt werden ).
Für eine Ausgabe in eine Postscriptdatei entfernt man das % vor der Zeile \usepackage[dvips]{graphicx} und setzt das % vor die darunterliegende Zeile. Anschließend kann man zweimal den Befehl latex und dann den Befehl dvips ausführen. Nun kann man das große f auch in einer Postscriptdatei sehen.
Der DVI-Betrachter kann das große f leider nicht darstellen.
Hinweis 2: Wir haben hier das Paket graphicx eingebunden. Dieses Paket wird in LaTeX Grundlagen Teil 2 behandelt. Dort geht es um Grafiken.
Hinweis 3: Ein mit dem Befehl \scalebox gesetzter Text wird nicht umgebrochen. Für einen zweizeiligen Text benötigt man also zweimal den Befehl \scalebox. Auch für den richtigen Abstand zwischen den Zeilen muß man selber sorgen. Wie das geht, steht oben unter der Überschrift: Größe des Zeilenumbruchs.
Maßeinheiten
Unter LaTeX gibt es div. Maßeinheiten die ich hier noch schnell aufliesten möchte, welche man zum Beispiel bei einem bestimmten Abstand mit \\[3cm] etc. verwenden kann.
Absolute Maße
- cm = Zentimeter
- mm = Millimeter
- pt = Punkt ( 1pt = 0.351 mm )
- in = Inch ( 1 Zoll = 2.54 cm )
Relative Maße
- ex = Die Buchstabenhöhe des buchstabens (x) in der derzeit verwendeten Schrift. Geeignet für vertikale Abstände.
- em = Die Buchstabenbreite des buchstabens ( M ) in der derzeit verwendeten Schrift. Geeignet für horizontale Abstände.
Grundlagen Teil 2
Die Fortführung des ersten Teils.
Weiteres Seitenlayout
Als Layout bezeichnet man eine Gesamterscheinung eines Medienproduktes.
Titel
Zum definieren eines Titels verwenden wir:
\begin{document}
\begin{titlepage} LaTeX \end{titlepage}
\end{document}
Dies würde eine zusätzliche Seite in unserem Dokument erstellen. Auf ihr wäre der angegebene Titel LaTeX zu sehen.
Titel, Autor, Datum
Eine weitere bequeme Möglichkeit für
- Titel
- Autor
- Datum
\documentclass[a4paper,10pt]{article}
\usepackage[ngerman]{babel}
\title{LaTeX \\ Artikel}
\author{Linux-Club.de}
\date{12.11.2005}
\begin{document}
\maketitle
Hier wäre nun der eigentliche Text unseres Dokumentes zu finden...
\end{document}
Die Titelseite wird an der Stelle erstellt an welcher der Befehl \maketitle im Dokument steht. Aussehen könnte dies dann so wie im Beispiel:
Neue Seite
Eine neue Seite kann ganz simpel mit dem Befehl:
\newpage
erstellt werden.
Seitennummerierung
Römische Seitenzahlen
Anstelle unserer üblichen Seitenzahlen, können auch Römische Zahlen verwendet werden, dazu folgendes in die Präambel schreiben.
\pagenumbering{roman}
Seitenzahl in Buchstaben
Wem es gefällt oder wer es benötigt kann anstelle von Seitenzahlen auch Buchstaben verwenden. Dazu diesen Eintrag in die Präambel mit aufnehmen.
\pagenumbering{Alph}
Seitennummerierung abschalten
Bei der Paginierung oder Seitennummerierung besteht die Möglichkeit, Seitenzahlen abzuschalten. D.h. Kopf und Fusszeilen bleiben vollständig leer. Empfehlenswert ist dies allerdings nicht immer, besonders bei der Verwendung eines Inhaltsverzeichnisses.
Beispiel:
\pagestyle{empty}
Würde die Seitenzahlen deaktivieren und kann schon in die Präambel geschrieben werden.
Wenn man nur bei einer einzelnen Seite die Seitennummerierung abschalten will, dann schreibt man den folgenden Befehl auf die Seite, die keine Nummerierung haben soll:
\thispagestyle{empty}
Auflistungen
Bei einer Auflistung haben wir verschiedene Möglichkeiten der Darstellung.
Punkt Auflistung
Der entscheidende Punkt ist hier itemize.
\begin{document}
\begin{itemize}
\item Zucker
\item Salz
\item Mehl
\end{itemize}
\end{document}
Zahlen Auflistung
Der wichtige Punkt ist hier enumerate, ansonsten bleibt alles beim alten.
\begin{document}
\begin{enumerate}
\item Zucker
\item Salz
\item Mehl
\end{enumerate}
\end{document}
Schlagwort Auflistung
Bei description kann das Schlag.- oder Stichwort selbst bestimmt werden, in diesem Falle ( Punkt 1 bis Punkt 3 ).
\begin{document}
\begin{description}
\item [Punkt 1] Zucker
\item [Punkt 2] Salz
\item [Punkt 3] Mehl
\end{description}
\end{document}
Fußnoten
Es ist recht simpel mit dem Befehl \footnote eine Fußnote einzufügen. Hierbei sollte allerdings beachtet werden, das bei:
- Report
- Book
die Fußnoten nicht komplett durchnummeriert werden, sondern Kapitelweise.
\begin{document}
Hier schreibe ich jetzt mal einen kleinen Text \footnote{Damit ist dieser Text gemeint}
bei dem ich eine Randnotiz einfügen möchte. Wie man nun sehen kann wurde
die Fußnote ganz unten auf dieser Seite eingefügt.
\end{document}
In der heutigen Typografie wird i.d.R. auf die untere Linie einer Fußnote verzichtet. Sie wird aus typografischer Sicht nicht benötigt und ist somit überflüssig. Um nun eine Fußnote ohne diese Linie erstellen zu können, setzen wir den Befehl: \let\footnoterule\relax voran.
\begin{document}
\let\footnoterule\relax
Das ist eine Fußnote \footnote{ohne Linie am Seitenfussende} in diesem Dokument.
\end{document}
Randnotiz
Eine Randnotiz kann man mit \marginpar hinzufügen.
\begin{document}
\noindent
Hier schreibe ich jetzt mal einen kleinen Text \marginpar{Notiz} bei dem ich eine
Randnotiz einfügen möchte. Wie man nun sehen kann wurde das Wort \textbf{Notiz}
als Randnotiz am Rechten Rand eingefügt.
\end{document}
Verweise bzw. Querverweise innerhalb eines Dokuments
Häufig nimmt man in Ausarbeitungen Bezug auf einen anderen Abschnitt der eigenen Ausarbeitung.
Siehe oben, Kapitel V Seite 27
Bei herkömmlichen Textverarbeitungen ist es schwierig, diese Verweise vor Fertigstellung der Arbeit zu setzen, da sich die angegebenen Seitenzahlen oder Kapitelbezeichnungen im Verlauf der Ausarbeitung des Dokuments noch ändern können.
LaTeX bietet hier eine sehr einfache und komfortable Möglichket an, schon beim Schreiben des Dokuments Verweise zu setzen, welche im Falle einer Änderung der Seiten- oder Kapitelzahl automatisch mit angepasst werden. Das zeitintensive Überprüfen und Erstellen von Querverweisen nach Fertigstellung einer Arbeit kann somit entfallen, da sich LaTeX selbständig um die Verwaltung und Anpassung der Verweise kümmert.
Verweise bestehen unter LaTeX aus zwei Teilen:
- dem Anker (Ort, auf den verwiesen wird) und
- dem Verweis selber.
Als Anker dient der folgende Befehl:
\label{Labelbezeichnung}
Dieser Anker ist mit einer frei wählbaren Labelbezeichnung an die Stelle des Textes zu setzen, auf die später verwiesen werden soll. Sinnvollerweise sollte man den Anker am Anfang des entsprechenden Absatzes platzieren, auf den später Bezug genommen wird.
Als Verweis auf diesen Anker (Label) dienen die Befehle:
\ref{Labelbezeichnung}
für einen Verweis auf einen Abschnitt und
\pageref{Labelbezeichnung}
für einen Verweis auf die entsprechende Seite im Dokument.
In den geschweiften Klammern ist hierbei die gleiche Labelbezeichnung zu wählen, welche man für den Anker vergeben hat. Auf diese Weise entstehen eindeutige Zuordnungen zwischen Anker und Verweis.
Anwendungsbeispiel:
Ein Anker wird so gesetzt:
Damit\label{Surrogation} die Erbschaft dem Nacherben möglichst ungeschmälert erhalten bleibt, gehören zur
Erbschaft nicht nur die vom Erblasser hinterlassenen Gegenstände, sondern auch deren Surrogate.
Verweisen kann man nun so:
Wie bereits oben geschildert (siehe oben, Kapitel \ref{Surrogation} auf Seite \pageref{Surrogation}) ...
Dies kann selbstverständlich auch in Fußnoten angewendet werden, wie das nachfolgende Beispiel zeigt:
Wie oben dargestellt wurde\footnote{Siehe oben, Abschnitt \ref{Surrogation}, Seite \pageref{Surrogation}}, ...
Zitate
Zitieren ist mit LaTeX kein Problem. Zitate werden mit LaTeX so dargestellt, dass bei dem zitierten Text beide Seiten des Textes im Vergleich zum übrigen Text eingerückt werden. Für Zitate kann man alternativ auf die Umgebungen quote oder quotation zugreifen.
Beispiel:
\begin{document}
Ein Zitat bedeutet, das ich einen Text oder eine entsprechende Textstelle von irgend wo anders übernehme.
\begin{quote}
Dies ist nun das Zitat.
\end{quote}
Ein Zitat wäre also ein expliziter Hinweis auf einen anderen Autoren. Man sollte aus Anstandsgrüden
bei einem Zitat die Quelle oder ein Literaturnachweis angeben.
\end{document}
Bei der Verwendung der Umgebung quote findet keine Einrückung der ersten Zeile statt.
Möchte man die erste Zeile eines Absatzes eingerückt haben, so muss anstelle der Umgebung quote die Umgebung quotation verwendet werden. Die Umgebung quotation eignet sich besser für längere Zitate, weche aus mehreren Absätzen bestehen und bei denen die ersten Zeilen neuer Absätze eingerückt werden sollen.
\begin{document}
Ein Zitat bedeutet, das ich einen Text oder eine entsprechende Textstelle von irgend wo anders übernehme.
\begin{quotation}
Dies ist nun das Zitat. Dies ist nun das Zitat. Dies ist nun das Zitat. Dies ist nun das Zitat. Dies ist nun das Zitat. Dies ist nun das Zitat.
\end{quotation}
Ein Zitat wäre also ein expliziter Hinweis auf einen anderen Autoren. Man sollte aus Anstandsgrüden bei einem Zitat die Quelle oder ein Literaturnachweis angeben.
\end{document}
Literaturverzeichnis
Das Einfügen von Literaturverzeichnissen ist ein bisschen aufwändiger, aber deshalb nicht schwerer. Wir müssen lediglich erst eine Umgebung für das Literaturverzeichnis schaffen.
\begin{document}
\begin{thebibliography}{------}
\end{thebibliography}
\end{document}
Mit den 6 Minuszeichen in den geschweiften Klammer, wird die spätere Breite des labels bestimmt, was natürlich entsprechend angepasst werden kann. Im Gesamten kann dies dann so aussehen:
\begin{thebibliography}{------}
\bibitem[1961]{1}
\textsc{Jan Tschichold}:
{\em Geschichte der Schrift in Bildern.}
Hamburg, 1961.
\end{thebibliography}
Info: Genaueres und mehr Informationen zum Theme Literaturverzeichniss ist im LaTeX WikiBook Literaturverzeichnisse beschrieben.
Abstände
Man kann unter LaTeX bei Texten oder auch Bildern bestimmte Abstände einfügen. Hier hat man dann die Wahl zwischen:
- mm
- cm
- pt
- em
- ex
Infos hierzu auch im Punkt Maßeinheiten vom Teil 1 der Grundlagen.
Abstand horizontal
Wir machen uns hierzu \hspace zunutze:
\begin{document}
Das ist mein Text in dem jetzt \hspace{3 cm} ein drei cm Abstand ist.
\end{document}
Die Maßeinheit ist hier cm.
Abstand vertikal
Beim vertikalen einfügen eines Abstandes verwenden wir den Befehl: \vspace.
\begin{document}
Das ist mein Text in dem jetzt
\vspace{1 cm}
ein ein cm Abstand ist.
\end{document}
Die Maßeinheit ist hier cm.
Mehrspaltiger Text
Für einen mehrspaltigen Text müssen wir zuerst ein weiteres Paket mit in die Präambel aufnehmen um dieses zu laden, der entsprechende Befehl heisst:
\usepackage{multicol}
Das Kommando zur Verwendung ist dann so aufgebaut:
\begin{multicols}{spaltenzahl}[titel]
\end{multicols}
Zwei Spalten
\begin{document}
\begin{multicols}{2}[Das ist der Titel]
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
\end{multicols}
\end{document}
Drei Spalten
\begin{document}
\begin{multicols}{3}[Das ist der Titel]
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
\end{multicols}
\end{document}
Weiteres
Weitere Möglichkeiten die wir haben sind zum Beispiel die Verwendung eines Striches zwischen den Spalten, genauso kann der Abstand zwischen diesen Spalten bestimmt werden oder die dicke des Trennstriches zwischen den Spalten.
Spaltenabstand
Hier wird zuerst angegeben, welchen Abstand wir zwischen unseren Spalten haben möchten.
\setlength{\columnsep}{1cm}
Strichdicke
Hier wird unsere Strichdicke in der Masseinheit pt = Punkt Grösse angegeben.
\setlength{\columnseprule}{0.5pt}
Beispiel Zweispaltig
\begin{document}
\setlength{\columnsep}{1cm}
\setlength{\columnseprule}{0.5pt}
\begin{multicols}{2}[Das ist der Titel]
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
\end{multicols}
\end{document}
Beispiel Vierspaltig
Es geht natürlich genauso bei noch mehr Spalten:
\begin{document}
\setlength{\columnsep}{1cm}
\setlength{\columnseprule}{0.5pt}
\begin{multicols}{4}[Das ist der Titel]
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
Hier ist ein Mehrspaltiger Text zu sehen.
\end{multicols}
\end{document}
Textrahmen
Ab und an wird auch mal ein Rahmen um einen Text benötig, ich möchte hier kurz zeigen wie das genau funktioniert.
frame
\begin{document}
\frame{Das ist ein Rahmen.}
\end{document}
fbox
\begin{document}
\fbox{Das ist ein Rahmen.}
\end{document}
framebox
\begin{document}
\framebox[5,0cm]{Das ist ein Rahmen.}
\end{document}
Spezielle Rahmen
Es gibt noch weitere spezielle Textrahmen für die man allerdings ein zusätzliches Paket benötigt. Um dieses Zusätzliche Paket verwenden zu können, schreiben wir wieder einen kleinen Eintrag in unsere Präambel:
\usepackage{fancybox}
OvalBox
\begin{document}
\ovalbox{Das ist ein ovaler Rahmen.}
\end{document}
ShadowBox
\begin{document}
\shadowbox{Das ist ein Rahmen mit Schatten.}
\end{document}
Grafik einbinden
Wer einmal eine Grafikdatei in sein Dokument einbinden muss ist hier richtig. Ich beschreibe ein paar unterschiedliche Wege dies zu tun, da es veraltete wie auch neuere Möglichkeiten gibt. Anbei bitte ich beide zu lesen.
epsfig
Die bereits ältere Methode welche aber dennoch funktioniert wäre epsfig welches ich als erstes vorstellen möchte. Zuerst muss in die Präambel der entsprechende Eintrag hinzugefügt werden damit das Paket geladen wird.
\usepackage{epsfig}
Nachdem der Eintrag in die Präambel hinzugefügt wurde, möchte ich darauf hinweisen, dass bei der Verwendung von epsfig nur Dateien im Encapsulated PostScript Format verwendet werden können. Dies soll heissen, das Bilder welche sich in einem anderen Dateiformat befinden bei einer gewünschten Verwendung erst umgewandelt werden müssen. Das Umwandeln aus einem *.jpeg, *.bmp, *.gif oder *.png geht recht einfach und sollte jede einfach Bildbearbeitungssoftware beherschen. Ich selbst empfehle für solche Dinge das Bildmanipulationsprogramm GIMP welches für die meisten Plattformen zur verfügung steht. Hat meine eine Grafik im *.eps Format forliegen, so kann diese mit dem Befehl \epsfig{file=< dateiname >.eps} eingebunden werden.
\epsfig{file=tux.eps}
Hierbei wird dann die Datei tux.eps in das Dokument eingebunden was dann so aussehen kann:
\documentclass[a4paper,10pt]{article}
\usepackage[ngerman]{babel}
\usepackage{epsfig}
\begin{document}
\epsfig{file=tux.eps}
\end{document}
Anstelle von *.eps Grafiken, können mit Hilfe von epsfig auch PS - PostScript Dateien eingefügt werden. Hierbei wird vollgender Befehl verwendet:
\epsfig{figure=beispiel.ps}
Hier würde die Datei beispiel.ps als Grafik in das Dokument eingebunden werden.
\documentclass[a4paper,10pt]{article}
\usepackage[ngerman]{babel}
\usepackage{epsfig}
\begin{document}
\epsfig{figure=beispiel.ps}
\end{document}
Bild Titel
Einer eingebundenen Grafik kann auch ein Titel mitgegeben werden was so aussehen würde. Zuerst sollte hierfür eine passende umgebung geschaffen werden.
\begin{document}
\begin{figure}
\end{figure}
\end{document}
Anschliessend kann man ein Bild mit Titel in das Dokument einfügen:
\begin{document}
\begin{figure}
\epsfig{file=tux.eps}
\caption{Das ist Tux der Pinguin}
\end{figure}
\end{document}
Grafiken Platzieren
Im Dokument eingefügte Grafiken können an verschiedenen Stellen platziert werden, hierfür werden drei Buchstaben verwendet:
- h
- t
- b
Mit (h) wird versucht die eingefügte Grafik an der Stelle im Dokument zu platzieren an dieser auch der entsprechende Befehl in der Quelldatei steht. Sollte der Befehl auf der 2ten von 3 Seiten sein, so wird versucht die Grafik auf der zweiten Seite einzufügen. Der Buchstabe (t) versucht die Grafik an den Anfang des entsprechenden dokumentes zu platzieren, das bedeutet das versucht wird die Grafik auf der ersten Seite darzustellen. Und zuguterletzt wird durch (b) versucht die Grafik an das Ende des Dokumentes zu setzen.
Hier zwei Beispiele dazu:
\begin{document}
Das ist ein Text...
\begin{figure}[h]
\epsfig{file=tux.eps}
\end{figure}
...und hier ein weiterer Text
\end{document}
\begin{document}
Das ist ein Text...
\begin{figure}[t]
\epsfig{file=tux.eps}
\end{figure}
...und hier ein weiterer Text
\end{document}
Bei b würde eine neue weitere letzte Seite erzeugt an diese die Grafik gestellt wird.
\begin{document}
Das ist ein Text...
\begin{figure}[b]
\epsfig{file=tux.eps}
\end{figure}
...und hier ein weiterer Text
\end{document}
Umranden
Umranden können wir mit \fbox{} so auch bei eingefügten Grafiken, hier ein Beispiel:
\begin{document}
Das ist ein Text...
\begin{figure}[h]
\fbox{
\epsfig{file=tux.eps}
}
\end{figure}
...und hier ein weiterer Text
\end{document}
Der Inhalt der geschweiften {..} Klammern beim Befehl fbox wird umrandet.
graphicx
Hier möchte ich nun die zweite und damit neuer Möglichkeit zeigen um Grafik in ein Dokument einzufügen. Als erstes müssen wir wieder ein Paket laden und hier den entsprechenden Befehl in die Präambel mit aufnehmen.
\usepackage{graphicx}
Mit dem Paket graphicx ist es uns möglich, weitere Dateiformate in unser Dokument einzufügen. Zu diesen geören zum Beispiel *.jpeg, *.png oder auch *.bmp. Der kleine aber feine Unterschied im Vergleich zu dem *.eps Format ist der, das die Bildgrösse expliziet mit angegeben werden muss. Bei einer *.eps Datei werden diese Informationen der Grafikdatei entnommen. Man gibt die Grösse folgendermaßen an:
[bb=0 0 165 198]
Wie im Beispiel zu sehen sind hier die Zahlen 230 und 276 vorhanden welche nichts anderes bedeuten als 230x276 PostScript-Punkte. Diese sogenannten PostScript-Punkte sind bitte nicht zu verwechseln mit den sogenannten Pixeln. Die beiden Grössen, PostScript-Punkte und Pixel lassen sich aber ineinander umrechnen. Hierbei entspricht 1PostScript-Punkte ungefähr 1,39 Pixel. Die Pixelgrösse mal 0,72 ergiebt dann die PS-Points. Die beiden Nullen müssen unbedingt angegeben werden. Hier noch einmal gerechnet anhand eines beispieles:
Unser Bild hat 230 x 276 Pixel, also rechnen wir:
230 x 0.72 = 165
276 x 0.72 = 198
Die 165x198 PostScript-Punkte sind dann wie oben im Beispiel zu schreiben.
Der gesammte Eintrag für ein Bild würde dann so aussehen:
\begin{document}
\begin{figure}
\includegraphics[bb=0 0 165 198]{tux.png}
\end{figure}
\end{document}
Hier würde dann die Grafikdatei tux.png in das Dokument eingefügt werden.
Bild Titel
Ein Titel für das Bild wird auf die gleiche Art und Weisse mit angegeben wie bei der Verwendung von epsfig.
\begin{document}
\begin{figure}
\includegraphics[bb=0 0 165 198]{tux.png}
\caption{Das ist Tux der Pinguin}
\end{figure}
\end{document}
Grafiken Platzieren
Auch hier wird genau so vorgegangen wie bereits im epsfig Teil weiter oben erwähnt. Durch genau das selbe Vorgehen, zeige ich hier nur ein Beispiel, undverweisse auf Punkt 1.3.1.2
\begin{document}
\begin{figure}[h]
\includegraphics[bb=0 0 165 198]{tux.png}
\caption{Das ist Tux der Pinguin}
\end{figure}
\end{document}
Umranden
Auch beim umranden der Grafik verwenden wir das selbe vorgehen wie unter epsfig Punkt 1.3.1.3
\begin{document}
Ich bin der Tux...
\begin{figure}[h]
\fbox{
\includegraphics[bb=0 0 165 198]{tux.png}
}
\end{figure}
...der Linux Tux aus Tuxhausen.
\end{document}
Grafik How-To
- Dominik Bischoff
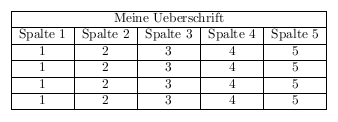
Tabellen
Ab und an ist es nötig in dem Dokument welches man gerade verfasst eine Tabelle zur besseren darstellung zu verwenden. Wie man genau eine Tabelle unter LaTeX in einem Dokument erstellt möchte ich hier zeigen.
Tabellenumgebung
Zuerst benötigen wir eine passende Umgebung für diese Tabelle, welche wir so erzeugen.
\begin{document}
\begin{tabular}{|l|c|r|}
\end{tabular}
\end{document}
Tabelleninhalt
Für jede Spalte benötigen wir einen Buchstaben, welche dann der Ausrichtung dienen. Ich habe in diesem beispiel drei Buchstaben angegeben für eine Tabelle mit drei Spalten. Getrennt werden diese drei Buchstaben durch den wagerechten Strich | welche die Begrenzung d.h. die Spaltenlinien darstellt. Die Bedeutung der drei Buchstaben ist folgende. Durch l was ein kleinen L ist wird der Inhalt linksbündig dargestellt. Durch das kleine c wird dieser genau in der Mitte, also Zentriert dargestellt. Das kleine c steht also für das Wort Center. Zuguterletzt wie soll es auch anderst sein, haben wir noch das kleine r als Buchstaben welches für einen rechtsbündigen Inhalt steht.
- l - left
- c - center
- r - right
Hier nun der Tabelleninhalt:
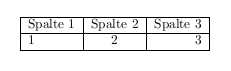
\hline Spalte 1 & Spalte 2 & Spalte 3\\ \hline 1 & 2 & 3\\ \hline
Wie in diesem Beispiel zu sehen, haben wir den Befehl \hline verwendet der eine horizontallinie ausgiebt. Spalte 1,Spalte 2 und Spalte 3 geben den Inhalt der drei Spalten aus. Genau soll das heissen, dass ihr die drei Wörter Spalte... ersetzten könnt durch irgend etwas anderes was später in der Tabelle stehen soll. Getrennt werden die einzelnen Spalten der Tabelle duch das UND Zeichen &. Die Zahlen 1 , 2 und 3 sind die Inhalte der zweiten Tabellenzeile und werden wie in der ersten Zeile durch das UND Zeichen & getrennt. Der Befehl \\ erzwingt einen Zeilenumbruch wie wir ihn schon zum Anfang des Buches kennengelernt haben.
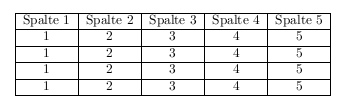
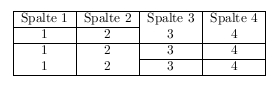
Tabellenbeispiel
Als fertiger Quelltext müsste dies dann so aussehen:
\begin{document}
\begin{tabular}{|l|c|r|}
\hline
Spalte 1 & Spalte 2 & Spalte 3\\ \hline
1 & 2 & 3\\ \hline
\end{tabular}
\end{document}
Grössere Tabelle
Hier ein weiteres Beispiel einer etwas grösseren Tabelle mit 5 Spalten und 5 Zeilen, aber genau der gleiche Prinzip bzw. das gleiche vorgehen. Die kleine Besonderheit wäre hier das im Vergleich zur ersten Tabelle der Inhalt aller Spalten durch c Zentreirt wurde.
\begin{document}
\begin{tabular}{|c|c|c|c|c|}
\hline
Spalte 1 & Spalte 2 & Spalte 3 & Spalte 4 & Spalte 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
\end{tabular}
\end{document}
Zusammenfügen von Zeilen
Wer in einer Tabelle div. Zeilen zusammen fügen muss, kann dies mit Hilfe von cline erledigen.
\begin{document}
\begin{tabular}{|c|c|c|c|}
\hline
Spalte 1 & Spalte 2 & Spalte 3 & Spalte 4 \\
\cline{1-2} 1 & 2 & 3 & 4 \\ \hline
1 & 2 & 3 & 4 \\
\cline{3-4} 1 & 2 & 3 & 4 \\ \hline
\end{tabular}
\end{document}
Wir geben in unserem Beispiel mit cline in den geschweiften Klammern an, dass wir die Zeilen 1 und Zeile 2 der Spalten 1 und Spalte 2 weiterhin mit einer Horizontallinie trennen, da der Befehl für die Horizontallinie in diesem Quellcode nicht mehr vorhanden ist, um zwei Zeilen zusammen zu fügen.
Schaut euch diesen Quellcode mit dem einer normalen Tabele weiter oben etwas genauer an und ihr werdet feststellen, das der Befehl \hline an zwei Stellen nicht mehr vorhanden ist.
Genau das gleiche gilbt auch fuer die Zeile 3 und Zeile 4 sowie fuer die Spalten 3 und Spalte 4.
Tabellen Überschrift
Wir haben nun vor einer Tabelle noch eine kleine mehrspaltige Überschrift zu geben. Dazu verwenden wir den Befehl \multicolumn. Wir geben in den ersten geschweiften Klammern die Spaltenanzahl ein, über die sich unsere Überschrift erstrecken soll. In den zweiten geschweiften Klammern geben wir unsere Ausrichtung an wie wir sie schon weiter oeben kennengelernt haben l,c,r. Und in den dritten geschweiften Klammern unseren Überschriftstext.
\multicolumn{Spaltenanzahl}{Ausrichtung}{Der Text}
In einer Tabelle kann dies dann zum Beispiel so aussehen:
\begin{document}
\begin{tabular}{|c|c|c|c|c|}
\hline
\multicolumn{5}{|c|}{Meine Ueberschrift}\\ \hline
Spalte 1 & Spalte 2 & Spalte 3 & Spalte 4 & Spalte 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
1 & 2 & 3 & 4 & 5\\ \hline
\end{tabular}
\end{document}
Linien
Um unter LaTeX Linien zu erstellen, nutzen wir den Befehl line mit den Angaben für die Horizontale, Vertikale Prosition und der Angabe für die Länge unserer Linie.
Die Syntax:
\line(h,v){l}
Das (h) steht für Horizontale das (v) für die Vertikale und das (l) für die Länge der Linie. Die Zahlenwerte reichen hierbei von -6 über 0 bis zu +6.
Horizontal
\line(1,0){50}
Vertikal
\line(0,1){50}
Pfeillinien
Anstelle von normalen Linien, können auch Pfeillinien gezeichnet werden, hierzu den Befehl \vector einsetzen.
Horizontal Pfeil
\begin{document}
\vector(1,0){20}
\end{document}
Vertikal Pfeil
\begin{document}
\vector(0,1){20}
\end{document}
Kordinatensystem
Für die Prositionierung von Grafiken wird unter LaTeX ein Kordinatensystem verwendet, welches eine Wagerechte X-Achse und eine Senkrechte Y-Achse verwendet. Der Schnittpunkt der beiden Achsen ist hier bei der Bezugspunkt (0,0). Mit dieser Möglichkeit, können alle Grafiken an eine bestimmte Prosition gebracht werden.
Picture Umgebung
Die Picture Umgebung definiert den Bereich in welchem die Liniengraphik verwendet werden kann.
\begin{picture}(Breite,Höhe)(X,Y)
\end{picture}
Die Breite und auch die Höhe im Befehl, geben die Breite und Höhe des Bildes an. x und y verschieben das Bild in horizontaler und vertikaler Richtung. Zudem sind die Werte (X und Y) optional.
Damit man sich so eine Umgebung besser vorstellen kann, empfehle ich hier am Anfang als kleine Hilfe einfach einen Rahmen herrum zeichenen zu lassen. Hier mal schnell ein kleines Beispiel mit einem Rahmen der durch \fbox erzeugt wird.
\begin{document}
\fbox{
\begin{picture}(180,100)
\end{picture}
}
\end{document}
Wie schon im Quelltext zu sehen, erstelle ich hier eine Umgebung welche eine Breitenangabe von 180 und eine Höhe von 100 hat. Nach Adam Riese und Eva Stein ist dies dann ein Rechteck welches breiter als höher ist.
In diese sogenatennte Picture Umgebung kann nun etwas gezeichnet werden, Linien, Pfeile oder auch Kreise sind möglich. Der Phantasie sind hier keine Grenzen gesetzt, einfach mal ein bisschen herrum spielen.
Objekt Positionieren
Um nun ein Objekt in einer Picture Umgebung genau positionieren zu können, verwenden wir den Befehl \put.
\put(X, Y){Objekt}
Mit dem Zahlenpaar für X und Y wird das Objekt an genau dieser Stelle in der Picture Umgebung dargestellt.
Beispiel Zeichnung
Wer nun das Kordinatensystem verstanden hat, weiss was eine Picture Umgebung ist und wie man Pbjektprositionen bestimmt, kann sich dieses Beispiel einmal ansehen. Alleine durch die hier in diesem Buch vorgestellten Befehle, ist man bereits in der Lage vollgendes Kordinatensystembeispielbild zu erstellen.
Hier mein Quelltext zum Bild:
\begin{document}
\begin{picture}(400,400)
\put(0.0,200.0){\line(6,0){400.0}}
\put(410.200,200.200){X-Achse}
\put(230.200,200.200){+1}
\put(260.200,200.200){+2}
\put(290.200,200.200){+3}
\put(320.200,200.200){+4}
\put(350.200,200.200){+5}
\put(380.200,200.200){+6}
\put(-45.200,200.200){X-Achse}
\put(160.200,200.200){-1}
\put(130.200,200.200){-2}
\put(100.200,200.200){-3}
\put(70.200,200.200){-4}
\put(40.200,200.200){-5}
\put(10.200,200.200){-6}
\put(200.0,200.0){\circle{10.0}}
\put(200.0,0.0){\line(0,6){400.0}}
\put(200.200,-20.200){Y-Achse}
\put(200.200,20.200){-6}
\put(200.200,50.200){-5}
\put(200.200,80.200){-4}
\put(200.200,110.200){-3}
\put(200.200,140.200){-2}
\put(200.200,170.200){-1}
\put(200.200,410.200){Y-Achse}
\put(200.200,380.200){+6}
\put(200.200,350.200){+5}
\put(200.200,320.200){+4}
\put(200.200,290.200){+3}
\put(200.200,260.200){+2}
\put(200.200,230.200){+1}
\end{picture}
\end{document}
Mit der ensprechenden Ausgabe:
Ja das Bild bzw. die Zeichnung ist nicht perfekt, aber das muss sie auch nicht sein. Mit dem hier beschriebenem soll man in der Lage sein einfache horizontale und vertikale linien und Pfeile zeichnen zu können. Vl. findet sich ja einer von euch Lesern der es perfekt hinbekommt...
Kreis
Einen einfachen kreis kann man mit dem Befehl \circle{25.0} erzeugen. In den geschweiften Klammern, wird der Durchmesser des Kreises angegeben. Dieser kann frei gewählt werden. Am besten verwendet man hier wieder eine Picture Umgebung deren Grösse wir festlegen. In diesem Beispiel nehme ich einfach mal 100 x 100. Wenn Wir dann einen Kreis zeichenen der einen Durchmesser von 25 hat, ist das ein viertel der grafischen Picture Umgebung und somit recht gross und deutlich anzusehen. Damit man die Picture Umgebung ebenfalls sehen kann, verwende ich hier zusätzlich noch eine fbox die wir weiter oben bereits kennengelernt haben und immer wieder praktisch auch als kleines Helferlein ist. Nach einer Fertigstellung kann die fbox ja wieder entfernt werden, wenn man keinen Rahmen mehr möchte.
\begin{document}
\fbox{
\begin{picture}(100,100)
\put(50.0,50.0){\circle{25.0}}
\end{picture}
}
\end{document}
Würfel Beispiel
Hier möchte ich mal ein Beispiel für einen Würfel zeigen.
\begin{document}
\fbox{
\begin{picture}(100,100)
\put(50.0,50.0){\circle*{25.0}}
\put(75.0,75.0){\circle*{25.0}}
\put(25.0,25.0){\circle*{25.0}}
\end{picture}
}
\end{document}
Hier noch ein weiterer Würfel:
\begin{document}
\fbox{
\begin{picture}(100,100)
\put(50.0,50.0){\circle*{25.0}}
\put(75.0,75.0){\circle*{25.0}}
\put(25.0,25.0){\circle*{25.0}}
\put(25.0,75.0){\circle*{25.0}}
\put(75.0,25.0){\circle*{25.0}}
\end{picture}
}
\end{document}
3D Würfel
In diesem Beispiel habe ich versucht einen Würfel in 3D darzustellen, ich hoffe mir ist es halbwegs gelungen.
\begin{document}
\fbox{
\begin{picture}(100,100)
\put(50.0,50.0){\circle*{25.0}}
\put(75.0,75.0){\circle*{25.0}}
\put(25.0,25.0){\circle*{25.0}}
\put(25.0,75.0){\circle*{25.0}}
\put(75.0,25.0){\circle*{25.0}}
\put(-6.0,102.0){\line(1,1){25.0}}
\put(106.0,102.0){\line(1,1){25.0}}
\put(106.0,-4.0){\line(1,1){25.0}}
\put(19.0,128.0){\line(1,0){112.0}}
\put(131.0,22.0){\line(0,1){105.0}}
\end{picture}
}
\end{document}
Hier noch ein weiterer kleiner 3D Würfel:
3D Würfel Beispiel
\begin{document}
\fbox{
\begin{picture}(100,100)
\put(-6.0,102.0){\line(1,1){25.0}}
\put(106.0,102.0){\line(1,1){25.0}}
\put(106.0,-4.0){\line(1,1){25.0}}
\put(19.0,128.0){\line(1,0){112.0}}
\put(131.0,22.0){\line(0,1){105.0}}
\put(-6.0,-4.0){\line(1,1){25.0}}
\put(19.0,22.0){\line(1,0){112.0}}
\put(19.0,22.0){\line(0,1){105.0}}
\end{picture}
}
\end{document}
Letztes Beispiel:
\begin{document}
\fbox{
\begin{picture}(100,100)
\put(-6.0,102.0){\line(1,1){25.0}}
\put(106.0,102.0){\line(1,1){25.0}}
\put(106.0,-4.0){\line(1,1){25.0}}
\put(19.0,128.0){\line(1,0){112.0}}
\put(131.0,22.0){\line(0,1){105.0}}
\put(-6.0,-4.0){\line(1,1){25.0}}
\put(19.0,22.0){\line(1,0){112.0}}
\put(19.0,22.0){\line(0,1){105.0}}
\put(33.0,50.0){\begin{Huge}\LaTeX\end{Huge}}
\end{picture}
}
\fbox{
\begin{picture}(100,100)
\put(-6.0,102.0){\line(1,1){25.0}}
\put(106.0,102.0){\line(1,1){25.0}}
\put(106.0,-4.0){\line(1,1){25.0}}
\put(19.0,128.0){\line(1,0){112.0}}
\put(131.0,22.0){\line(0,1){105.0}}
\put(-6.0,-4.0){\line(1,1){25.0}}
\put(19.0,22.0){\line(1,0){112.0}}
\put(19.0,22.0){\line(0,1){105.0}}
\put(42.0,50.0){\begin{Huge}\TeX\end{Huge}}
\end{picture}
}
\fbox{
\begin{picture}(100,100)
\put(-6.0,102.0){\line(1,1){25.0}}
\put(106.0,102.0){\line(1,1){25.0}}
\put(106.0,-4.0){\line(1,1){25.0}}
\put(19.0,128.0){\line(1,0){112.0}}
\put(131.0,22.0){\line(0,1){105.0}}
\put(-6.0,-4.0){\line(1,1){25.0}}
\put(19.0,22.0){\line(1,0){112.0}}
\put(19.0,22.0){\line(0,1){105.0}}
\put(33.0,50.0){\begin{Huge}\LaTeX\end{Huge}}
\end{picture}
}
\fbox{
\begin{picture}(100,100)
\put(-6.0,102.0){\line(1,1){25.0}}
\put(106.0,102.0){\line(1,1){25.0}}
\put(106.0,-4.0){\line(1,1){25.0}}
\put(19.0,128.0){\line(1,0){112.0}}
\put(131.0,22.0){\line(0,1){105.0}}
\put(-6.0,-4.0){\line(1,1){25.0}}
\put(19.0,22.0){\line(1,0){112.0}}
\put(19.0,22.0){\line(0,1){105.0}}
\put(42.0,50.0){\begin{Huge}\TeX\end{Huge}}
\end{picture}
}
\end{document}
Komando Definition
Ab und an hat man etwas grösseres oder etwas das sich sehr oft wiederholt und man möchte dieses nicht immer wieder schreiben müssen. Für so einen Fall, können wir ein eigenes neues Komando definieren das dann die gewünschten Zeilen einfügt oder ausführt.
Angenommen ich schreibe einen Text in dem ich zum Beispiel sehr oft eine Nummer oder einen langen Namen schreiben muss, dann kann ich mir das Leben mit dem Befehl \newcommand etwas vereinfachen.
\begin{document}
\newcommand{\n}{0100101}
Nun kann ich meinen Text schreiben in dem ich nicht mehr
die Nummer \n ~schreiben muss.
\end{document}
Wie im Beispiel zu sehen, erstellen wir einen neuen Befehl oder ein neues Komando \n an jeder Stelle im Quelltext wo das neue Komando steht wird dann die entsprechende Aktion oder Anweisung durchgeführt. Un unserem Fall sagen wir das \n eine Nummer {0100101} ist welche wir nicht immer wieder neu schreiben wollen. Nun wird wie im Beispiel zu sehen, an der Stelle wo unser neues Komando steht die Nummer ausgegeben.
Querformat (Verschiedene Möglichkeiten zur Einstellung von Seitenrändern)
Üblicherweise wird Papier im Hochformat beschrieben, denn ein Text im Hochformat ist viel leichter lesbar, als ein im Querformat geschriebener Text. Es wäre für das menschliche Auge geradezu eine Qual, wenn es einen Text im Querformat lesen müsste. Sollte man doch einmal ein Blatt im Querformat beschreiben müssen, verwendet man Spalten, damit die Zeilen nicht zu lang werden.
Manchmal ist Querformat jedoch sehr sinnvoll. Etwa wenn man eine Tabelle setzen möchte, einen Stundenplan oder einen Diensplan für einen ganzen Monat. Eine solche Tabelle kann breiter als hoch sein.
Man muß hier zwischen Postscript und PDF unterscheiden. Falls man ein PDF im Querformat wünscht, muß man in seinem LaTeX Code folgende Zeile einfügen:
\usepackage[pdftex,landscape]{geometry}
falls man ein Postscriptdokument wünscht, muß die Zeile so lauten:
\usepackage[dvips,landscape]{geometry}
Der Parameter landscape zeigt LaTeX an, dass es sich um ein Dokument im Querformat handelt. Der Parameter pdftex sorgt dafür, dass das fertige PDF im Querformat angezeigt wird. Und der Parameter dvips sorgt dafür, dass das Dokument auch im DVI-Betrachter als Querformat angezeigt wird.
Hier eine Musterkonfiguration: ( Eingestellt auf PDF )
\documentclass[12pt, a4paper] {article}
\usepackage[pdftex,landscape]{geometry}
%\usepackage[dvips,landscape]{geometry}
\usepackage[ngerman]{babel}
\usepackage[utf8]{inputenc}
\oddsidemargin-2.2cm
\textwidth29cm
\headheight0cm
\topmargin-3cm
\textheight20cm
\begin{document}
\pagestyle{empty}
Hier kann etwas stehen.
\end{document}
In dieser Musterkonfiguration wurde eine etwas grössere Schrift (12pt) gewählt. Die Anweisung
- \oddsidemargin gibt die Breite des linken Randes an. Der Wert kann negativ werden, wenn man einen sehr schmalen Rand haben möchte. Die Anweisung
- \textwidth gibt an, wie breit der Text sein darf,
- \topmargin bestimmt die Höhe des oberen Randes,
- \headheight gibt die Höhe der Kopfzeile an,
- \textheight gibt an, wie hoch der bedruckte Bereich auf dem Papier sein darf.
Weiter findet man nach \begin{Dokument} die Anweisung \pagestyle{empty}. Diese Anweisung leert die Kopf- und Fußzeile, und entfernt außerdem die Seitennummerierung.
In dieser Vorlage sind die Grössen so eingestellt, dass fast das gesamte Blatt Papier bedruckt wird. Es bleibt fast kein Rand. Die Vorlage ist auf PDF - Latex eingestellt. Falls man ein DVI - Dokument wünscht, macht man die entspechende Zeile scharf, indem man das (%) Zeichen entfernt. Statt dessen setzt man ein (%) Zeichen vor die darüberliegende Zeile.
Hinweis 1: Durch das % Zeichen wird ein Kommentar eingeleitet. LaTeX ignoriert alles, was sich nach einem % Zeichen befindet. Wenn man ein % Zeichen setzen möchte, muß man dies ausdrücklich anweisen. Und zwar durch \% . Dann wird das % Zeichen nicht ignoriert.
Hinweis 2: Grundsätzlich sollten Befehle wie \oddsidemargin und Konsorten nicht mehr verwendet werden. Man sollte die Seitenränder statt dessen im Paket geometry angeben. Das Paket geometry wird in "Grundlagen Teil 1" unter der Überschrift "Seitenränder" beschrieben. Ich habe diese Befehle nur deshalb verwendet, weil ich sie im Buch "Linux" von Michael Kofler so gelernt habe. Viel einfacher ist es, wenn man \oddsidemargin und Konsorten weg lässt, und die Seitenränder so angibt:
\usepackage[pdftex, landscape, left=5pt, right=5pt, top=5pt, bottom=5pt]{geometry}
Und für die richtige Ausgabe im DVI-Format ersetzt man hier pdftex durch dvips.
Die Musterkonfiguration sieht dann so aus:
\documentclass[12pt, a4paper] {article}
\usepackage[pdftex, landscape, left=5pt, right=5pt, top=5pt, bottom=5pt]{geometry}
%\usepackage[dvips, landscape, left=5pt, right=5pt, top=5pt, bottom=5pt]{geometry}
\usepackage[ngerman]{babel}
\usepackage[utf8]{inputenc}
\begin{document}
\pagestyle{empty}
Hier kann etwas stehen.
\end{document}
Und hier endlich die Ausgabe unserer Vorlage:
Mathematische Formeln
Umgebungen für mathematische Formeln
Formeln im Fließtext
Um eine Formel im Text zu setzten gibt es die $Formel$ Umgebung.
Beispiel:
\begin{document}
Dieser Bruch $\frac{1}{x^2}$ passt genau in eine Zeile.
\end{document}
Formeln werden in dieser Umgebung etwas zusammengestaucht. Dadurch leidet etwas die Schönheit der Formel. Wenn man mehr Platz hat, nimmt man besser eine Umgebung für abgesetzte Formeln.
Abgesetzte Formeln
Hier gibt es eine ganze Reihe von Umgebungen. Zum Beispiel:
\begin{document}
\begin{displaymath}
Formel
\end{displaymath}
\end{document}
\begin{document}
\begin{equation}
Formel
\end{equation}
\end{document}
\begin{document}
\begin{eqnarray}
Formel
\end{eqnarray}
\end{document}
Es werden noch zahlreiche weitere Umgebungen durch das Paket amsmath bereitgestellt. Man kann es durch die Anweisung
\usepackage[optionale Parameter]{amsmath}
in der Präambel einbinden. Das Paket enthält einige Ergänzungen zum LaTeX Standard.
Diese Umgebungen wirken alle leicht unterschiedlich. Die equation-Umgebung etwa arbeitet genau wie die displaymath-Umgebung, setzt aber zusätzliche Nummerierungen an die Formeln. Die eqnarray-Umgebung eignet sich zum Setzen von Gleichungssystemen. Welche Umgebung man verwendet, hängt nicht zuletzt auch vom persönlichen Geschmack ab. In dieser Einführung werden wir uns auf die Umgebung
\begin{document}
\begin{displaymath}
Formel
\end{displaymath}
\end{document}
beschränken. Diese Umgebung kann man auch kürzer
\[ Formel \]
schreiben.
Hinweis: Falls man das Paket amsmath verwenden möchte ( was empfohlen wird ), sollte man unbedingt die Kurzschreibweise \[ Formel \] benutzen, da sie kompatibel zum Paket amsmath ist. Die Schreibweise \begin{displaymath} Formel \end{displaymath} ist leider nicht kompatibel zum Paket amsmath. Die hier vorgestellten Formeln funktionieren allerdings unter beiden Schreibweisen gleich.
Beispiele
Brüche
Um einen Bruch zu setzen, gibt es das Kommando \frac{Zaehler}{Nenner}
Beispiel:
\begin{document}
\begin{displaymath}
\frac{1}{1+1} = \frac{1}{2}
\end{displaymath}
\end{document}
Wurzeln
Um eine Wurzel zu setzen, gibt es das Kommando \sqrt[..]{..} Beispiel: Die vierte Wurzel aus 81 ist 3.
\begin{document}
\begin{displaymath}
\sqrt[4]{81}=3
\end{displaymath}
\end{document}
Eine quadratische Wurzel setzt man so: \sqrt{..}
\begin{document}
\begin{displaymath}
\sqrt{2}=1,4142
\end{displaymath}
\end{document}
Das Summenzeichen
Das Summenzeichen wird duch den Befehl \sum gesetzt.
\begin{document}
\begin{displaymath}
\sum
\end{displaymath}
\end{document}
Hoch- und Tiefstellen
Mit dem ^ wird etwas hochgestellt. Mit dem _ wird etwas tiefgestellt. Soll mehr als ein Zeichen hoch- oder tiefgestellt werden, müssen diese Zeichen in geschweifte Klammern { } gesetzt werden.
Beispiel:
\begin{document}
\begin{displaymath}
\sum_{i=1}^n
\end{displaymath}
\end{document}
Vergisst man die Klammern um {i=1}, so wie im folgenden Beispiel, passiert das:
\begin{document}
\begin{displaymath}
\sum_i=1^n
\end{displaymath}
\end{document}
Integrale
Das Integralzeichen erhält man duch den Befehl \int
Beispiel:
\begin{document}
\begin{displaymath}
\int_a^bf(x)dx
\end{displaymath}
\end{document}
Das Produktzeichen
Das Produktzeichen erhält man durch den Befehl \prod
Beispiel:
\begin{document}
\begin{displaymath}
\prod_{i=1}^3 i = 1*2*3 = 3!
\end{displaymath}
\end{document}
Binomialkoeffizienten
Die Binomialkoeffizienten n über k erhält man durch den Befehl {n \choose k}
Beispiel:
\begin{document}
\begin{displaymath}
{n \choose k} = \frac{n!}{k!(n-k)!}
\end{displaymath}
\end{document}
Limes
Der Limes wird durch das Kommando \lim gesetzt. Der Pfeil nach rechts wird durch das Kommando \rightarrow gesetzt. Das "Unendlich"-Zeichen wird durch das Kommando \infty gesetzt.
\begin{document}
\begin{displaymath}
\lim_{x\rightarrow\infty} \frac{1}{x} = 0
\end{displaymath}
\end{document}
Klammerungen in Formeln
Normale Klammern (die \left \right Umgebung)
Klammern setzt man am besten mit der \left \right Umgebung, denn dann passt sich die Größe der Klammern an die Größe der Formeln an. Die Klammern werden direkt nach \left oder \right gesetzt. Man kann alle möglichen Klammern nehmen. Etwa (), [], {}, <>. Auch den senkrechten Strich | kann man verwenden. Man muß die Klammern nicht paarweise verwenden. Auch (} ist möglich. Und dies ][ ist möglich. Die Befehle \left \right müssen immer paarweise vorkommen. Will man aber etwa nur eine sich öffnende Klammer haben, so setzt man nach dem \right einen Punkt. \right. (Punkt)
Hinweis: Wenn man geschweifte Klammern {} verwenden will, muß man ein \ voranstellen oder man verwendet die Kommandos \lbrace und \rbrace für die linke und rechte geschweifte Klammer.
Beispiel: Eine runde und eckige Klammer um unser Integral.
\begin{document}
\begin{displaymath}
\left( \int_a^bf(x)dx \right>
\end{displaymath}
\end{document}
Ein weiteres Beispiel für die \left \right Umgebung findet man im Abschnitt über Matrizen.
Klammerung von unten (\underbrace)
Der Befehl \underbrace{} klammert von unten nach oben.
Beispiel 1:
\begin{document}
\begin{displaymath}
\underbrace{a+b}
\end{displaymath}
\end{document}
Beispiel 2: (Rechenaufgabe des Gauss)
\begin{document}
\begin{displaymath}
\sum_{i=1}^{100} i = 1+2+\dots+99+100 =
\underbrace{1+100}_{101} + \underbrace{2+99}_{101} + \dots +\underbrace{50+51}_{101}
= 50*101 = 5050
\end{displaymath}
\end{document}
Klammerung von oben (\overbrace)
Der Befehl \overbrace{} klammert von oben nach unten.
Beispiel:
\begin{document}
\begin{displaymath}
\overbrace{a+b}
\end{displaymath}
\end{document}
Horizontale Abstände in Formeln
Abstände
Sehr selten ist man mit den von LaTeX gewählten Abständen nicht zufrieden. Um diese Abstände zu vergrößern, gibt es unter anderem folgende Befehle:
- \, (kleiner Abstand)
- \: (etwas größerer Abstand)
- \quad (großer Abstand)
- \qquad (2 * quad)
Darüber hinaus gibt es den Befehl \hspace{abstand}. Hier kann man den Abstand zum Beispiel in pt (Breite eines Punktes), mm oder cm angeben. Durch die Anweisung \hspace{2cm} wird also ein 2 cm breiter horizontaler Abstand eingefügt.
Durch die Anweisung \! kann man einen Abstand verringern.
Beispiel (Dichte der Normalverteilung )
(Siehe Kleine Enzyklopädie Mathematik 2. Auflage 1984 Verlag Harry Deutsch. Seite 642)
Die Dichte der Normalverteilung kann man dann durch folgenden Code setzen:
\begin{document}
\begin{displaymath}
p(x) = \frac{1}{a\sqrt{2\pi}} e^{-\frac{(x-b)^2}{2a^2}}
\end{displaymath}
\end{document}
Und hier das Gleiche. Ein kleiner Abstand wurde eingefügt.
\begin{document}
\begin{displaymath}
p(x) = \frac{1}{a\sqrt{2\pi}} \, e^{-\frac{(x-b)^2}{2a^2}}
\end{displaymath}
\end{document}
Ob man es wirklich für nötig hält, hier einen Abstand einzufügen, ist natürlich Geschmackssache. Ein weiteres Beispiel für zusätzlich eingefügten Abstand findet man im gleich folgenden Beispiel Indikatorfunktion. Dort ist es aber wirklich nötig.
Die Array-Umgebung
Abschnittsweise definierte Funktionen (Indikatorfunktion)
Um eine abschnittsweise definierte Funktion zu setzten, benötigt man die Umgebung
\begin{document}
\begin{displaymath}
\begin{array}{Spalten}
Tabellenartige Formel
\end{array}
\end{displaymath}
\end{document}
Mit dieser Umgebung setzen wir eine Tabelle. Das & Zeichen trennt die Spalten. Für eine 2-Spaltige Tabelle geben wir hier für Spalten cc ein. Das zeigen wir gleich am Beispiel Indikatorfunktion. Wir haben hier eine sich öffnende linke Klammer. Die rechte Klammer wurde unsichtbar gemacht (der Punkt nach right). Zeilen schließt man durch \\ ab.
Beispiel: (Indikatorfunktion)
\begin{document}
\begin{displaymath}
1_{[0,1]}(x) =
\left\{
\begin{array}{cc}
1 & falls \quad x \in [0,1] \\
0 & sonst
\end{array}
\right.
\end{displaymath}
\end{document}
Zwischen \begin{array}{cc} und \end{array} wird hier eine 2-Spaltige Tabelle gesetzt. Die Spalten werden durch das & Zeichen getrennt. In der ersten Spalte stehen die 1 und die 0, in der zweiten Spalte stehen die Bedingungen. Der Befehl \in erzeugt das ∈ Zeichen. Statt des Buchstabens c kann man auch l oder r schreiben. Es wird dann in der jeweiligen Spalte eine linksbündige oder rechtsbündige Ausgabe erzeugt. Durch das c erhält man eine zentrierte Ausgabe.
Matrizen
Auch für Matrizen verwenden wir die array-Umgebung. Für eine 3x3-Matrix benötigen wir 3 Spalten. Deshalb setzen wir 3 c ein. Auch hier werden Zeilen durch \\ getrennt. Die Spalten werden durch das & Zeichen getrennt. Es ist auch noch ein schönes Beispiel für die \left \right Umgebung. Hier ist die Matrix:
\begin{document}
\begin{displaymath}
A =
\left(
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}
\right)
\end{displaymath}
\end{document}
Gleichungen
Wir lösen eine einfache Gleichung mit einer Unbekannten. Um sie zu setzen, verwenden wir eine array-Umgebung mit 5 Spalten. Die erste Spalte ist rechtsbündig gesetzt, die zweite zentriert, die dritte linksbündig, die vierte zentriert und die fünfte Spalte ist wieder rechtsbündig gesetzt:
\begin{document}
\begin{displaymath}
\begin{array}{rclcr}
3x + 4 & = & 2x + 11 & | & -4 \\
3x & = & 2x + 7 & | & - 2x \\
x & = & 7 & &
\end{array}
\end{displaymath}
\end{document}
In einer sechsten Spalte könnte man auch Zeilennummerierungen einfügen. Man könnte sie rechtsbündig ( r ) setzen.
Hinweis: Einen Abstand erzeugt man durch \quad (oder auch \qquad)
Fortgeschrittene
In diesem Bereich Anwendungen für Fortgeschrittene soll es ein bisschen weiter gehen wie das was wir in den Grundlagen dieses Wiki Books Teil 1 und Teil 2 gelernt haben. Fortgeschrittene soll nicht heissen das es schwerer oder kompliziert wird und nur von Profis zu verstehen ist. In diesem Bereich sollen Dinge gezeigt und erklärt werden welche man nicht unbedingt bei der alltäglichen Arbeit benötigt oder dafür wissen muss. Würde dieser Teil so geschrieben werden das er nur von Profis verstanden würde, so wäre ich ein schlechter Autor und dies ein schlechtes Wiki.
Für was ?
Jeder der diesen Teil des Wiki Books liest, wird mit dem Textsatzprogramm LaTeX bereits gearbeitet haben.
Ich stelle nun einfach mal die Frage, für was genau verwendet ihr eigentlich LaTeX ?
Natürlich wird hier an erster Stelle die Antwort stehen:
- Um einen Text in Form von Artikeln, Berichte, Briefe oder sogar eines Buches schreiben zu können.
An zweiter Stelle kommt vermutlich:
- Um den zu verfassenden Text sauber, einheitlich und richtig darstellen zu können.
Ersteres ist natülich ganz klar: Wir benötigen kein Textsatzsystem, wenn wir nichts zu verfassen haben. Beim zweiten Punkt, der Darstellung
unseres Textes, den wir verfassen, kann LaTeX uns eine Menge an Arbeit abnehmen. Hierzu gehört zum Beispiel das Setzten von Überschriften an
die jeweils richtige Stelle. Das richtige Darstellen von beispielsweise Randnotizen oder auch Fußnoten. Genauso wird dafür gesorgt, dass wir
immer die entsprechend vorgegebenen oder bereits von Hand eingestellten Seitenränder, etc., einhalten, oder dass unser Satzspiegel an der richtigen
Stelle in unserem Dokument platziert wird.
Schön und gut, wenn uns so viel an Arbeit abgenommen wird, doch sollten wir nicht auch selbst wissen was mit einer "Nutzflache" im Dokument gemeint ist, wie sie aufgebaut ist, an welche Stelle sie steht und was darum herum existiert? Was ist ein Außensteg etc.?
Seitenaufbau
Was gibt es alles auf einer Seite bzw. kann es dort geben und wo wird es platziert. Diese Fragen soll hier schön verständlich beantwortet werden.
Zu einer Seite gehören oder können gehören:
- Satzspiegel
- Paginierung
- Kopfsteg
- Marginalien
- Toter Kolumnentitel
- Lebender Kolumnentitel
- Fußsteg
- Bundsteg
- Außensteg
Satzspiegel
Als Satzspiegel einer Seite, wird auch die sogenannte Nutzfläche in der Typografie bezeichnet. Wenn ich eine Seite mit einem niedergeschriebenem Text nehme, und diesen eigentlich Text mit einem Rahmen umrahme, sehe ich was ein Satzspiegel ist. Zum Satzspiegel gehören in der Regel keine Seitennummern ( Paginierungen ). Genausowenig gehört kein toter Kolumnentitel zum Satzspiegel. Marginalien ( Randnotzien ) gehören ebenso nicht zu einem Satzspiegel, zudem befindet sich ein Satzspiegel in einem Dokument stehts an ein und der selben Stelle. Das heisst, er kann nicht nach belieben auf jeder Seite hin und her geschoben werden. Desweitern wird ein Satzspiegel begrenzt durch die sogenanten Stege, welche den unbedruckten Bereich zwischen dem Satzspiegel und dem Rand darstellen. Die Spalten auch Kolumnen genannt mit dem eigentlichen Text oder auch Grafiken und Bildern gehören mit zum Satzspiegel. Gleiches gilt auch für die Fußnoten welche mit zum Satzspiegel gerechnet werden.
Paginierung
Mit Paginierung bezeichnet man das festlegen der Stelle an der die Seitennummer des Dokumentes sein soll. Eine Seite kann durchaus an mehreren Stellen die Seitennummer haben. Allerdings ist zu beachten, das die Stelle der Seitennummer an der diese angebracht ist durchgehen durch das gesamte Dokument fliesst. Dies soll heissen, das die Seitenzahl oder Seitenzahlen immer an der selben Stelle der einzelnen Seiten zu finden sein sollen.
Kopfsteg
Mit dem Wort Kopfsteg wird ebenfalls der "Obere Rand" bezeichnet. Dies ist der Bereich welche von der oberen wagerechten Kante des Blattes bis zum Satzspiegel reicht. Mit in den Kopfsteg kann zum Beispiekl auch der toter Kolumnentitel geschrieben werden. Hierbei sollte allerdings beachtet werden, das dieser nicht mit in den linken und rechten Außensteg gelangt, genauso wenig in den Bundsteg bei Büchern.
Marginalien
Marginalien sind wie Randnotzien kleine leichte Ergänzungen zum Text welche meistens im rechten Außensteg ( Rechter Rand ) zufinden sind. Die kleinen leichten Marginalien werden in der Regel nicht mit zum Satzspiegel dazu gerechnet. Es können auch nur Symbole oder andere kleine Elemente sein.
Viele oder sehr grosse Marginalien welche viel Platz benötigen werden mit zum Satzspiegel gerechnet.
Der Grund weshalb Marginalien meistens auf die Rechte Seite geschrieben werden liegt daran das wenn man das fertige Blatt ebheften würde durch den Rand welcher auf der linken Seite entsteht einen Bereich ( Bundsteeg z.B. bei einem Buch ) hat der sehr schlecht ins Auge fällt. Man könnte die Marginalien aber auch anstelle der rechten auf die Linke Seite schreiben wenn man dies wünscht.
Toter Kolumnentitel
Der sogenannte tote Kolumnentitel wird nicht mit zum Satzspiegel gezählt und ist bzw. sollte immer durch das gesamte Dokument an einer festen Stelle stehen. Desweiteren befindet sich der toter Kolumnentitel entweder im oberen oder unteres Rand bzw. im Bereich des Kopf- u. Fußsteges. Er sollte klein, leicht und dezent gehalten werden, so das er den eigentlichen Satzspiegel nicht stört.
Lebender Kolumnentitel
Der lebender Kolumnentitel ist Teil des Satzspiegels und wird in dessen erste Zeile geschrieben. Dieser lebender Kolumnentitel sollte vortlaufend im Dokument ebenfalls immer an der selben Stelle zu finden sein. Sollte auf einer Seite der lebender Kolumnentitel und oder eine Überschrift an der selben Stelle stehen, so fällt der lebender Kolumnentitel weg. Sollte bei der Paginierung eine Seitenzahl mit in den Bereich des Satzspiegels kommen, so gehört diese Seitenzahl mit in die selbe Zeile innerhalb des Satzspiegels wie auch der lebender Kolumnentitel.
Fußsteg
Mit Fußsteg wird ebenfalls der untere Rand bezeichnet. Dieser ist der Bereich von der waagerechten Seite des Blattes bis zum Satzspiegel auf der Seite. Mit in den Fußsteg kann zum Beispiekl auch der toter Kolumnentitel geschrieben werden. Hierbei sollte allerdings beachtet werden, das dieser nicht mit in den linken und rechten Außensteg gelangt, genauso wenig in den Bundsteg bei Büchern.
Bundsteg
Der Bundsteg ist der Bereicht welcher beim erstellen eines Buches für die Bindung benötigt wird. In einem Buch habe ich so auf der rechten Buchseite einen Bundsteg auf der linken Seite des Blattes, und auf der Linken seite der Buchseite einen Bundsteg auf der Rechten Seite des Blattes. Zudem ist der Bundsteg ein später nicht mehr sichtbarer Bereicht, da dieser für die Buchbindung verwendet wird.
Außensteg
Der Außensteg ist der Bereich, welcher auch als äußerer Rand bezeichnet wird. Es ist der Teil, welcher von der senkrechten Papierkante am linken wie auch am rechten Rand bis zum Satzspiegel reicht.
Darstellungsbeispiel
Hier wurden nun mehrere Dinge genannt und mit Hilfe von wörtern beschrieben. Da es für manche jedoch einfacher ist dies zu verstehen wenn sie es bildlich vor sich haben, so habe ich das ganze mal schnell in LaTeX geschrieben um es verständlicher zu machen. Der eigentliche Quelltext befindet sich im Anschluss unter dem Bild. Hierbei sollte allerdings erwähnt werden, das ich die Paginierung ( Seitennummerierung ) im Beispiel weg gelassen habe. Einzig die Paginierung im Satzspiegel befindet sich im Beispiel.
Quellcode der Darstellung:
\begin{document}
\fbox{
\begin{picture}(331,594)
\put(-6.0,610.0){\line(0,1){10.0}}
\put(337.0,610.0){\line(0,1){10.0}}
\put(122.0,610.0){Kolumnentitel tot}
\put(80.0,610.0){$ \leftarrow $}
\put(40.0,610.0){$ \leftarrow $}
\put(240.0,610.0){$ \rightarrow $}
\put(280.0,610.0){$ \rightarrow $}
\put(0.0,575.0){Kolumnentitel lebend}
\put(+278.0,575.0){Paginierung}
\put(-6.0,560.0){\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots\dots}
\put(140.0,300.0){Satzspiegel}
\put(80.0,300.0){$ \leftarrow $}
\put(240.0,300.0){$ \rightarrow $}
\put(162.0,350.0){$ \uparrow $}
\put(162.0,250.0){$ \downarrow $}
\put(-6.0,-20.0){\line(0,1){10.0}}
\put(337.0,-20.0){\line(0,1){10.0}}
\put(122.0,-20.0){Kolumnentitel tot}
\put(80.0,-20.0){$ \leftarrow $}
\put(40.0,-20.0){$ \leftarrow $}
\put(240.0,-20.0){$ \rightarrow $}
\put(280.0,-20.0){$ \rightarrow $}
\put(-72.0,300.0){Aussensteg}
\put(-69.0,290.0){Bundsteg}
\put(-84.0,300.0){$ \leftarrow $}
\put(-22.0,300.0){$ \rightarrow $}
\put(398.0,300.0){Aussensteg}
\put(375.0,300.0){$ \leftarrow $}
\put(459.0,300.0){$ \rightarrow $}
\put(-55.0,-3.0){\line(1,0){10.0}}
\put(-65.0,-80.0){Fusssteg}
\put(-77.0,-90.0){Unterer Rand}
\put(-52.0,-55.0){$ \uparrow $}
\put(-52.0,-115.0){$ \downarrow $}
\put(-55.0,597.0){\line(1,0){10.0}}
\put(-65.0,670.0){Kopfsteg}
\put(-75.0,660.0){Oberer Rand}
\put(-52.0,685.0){$ \uparrow $}
\put(-52.0,647.0){$ \downarrow $}
\put(367.0,450.0){Marginalien}
\put(353.0,450.0){$ \leftarrow $}
\put(422.0,450.0){$ \rightarrow $}
\put(440.0,448.0){\line(0,1){10.0}}
\put(345.0,448.0){\line(0,1){10.0}}
\end{picture}
}
\end{document}
Satzspiegel
Wir haben im oberen Teil erfahren was ein Satzspiegel ist und was er beinhalten kann. Nun geht es darum den Satzspiegel an die richtige Stelle auf einer Seite zu setzen und seine Prosition zu bestimmen.
Konstruktionsverfahren
Für die Bestimmung des Satzspiegel gibt es verschiedene Verfahren.
- Goldener Schnitt
- Rastersystemverfahren
Hinweis: Die hier gezeigten Beispiele sind geeignet für einen beidseitigen Druck wie beispielsweisse bei Büchern etc.
Für Briefe oder Manuskripte welche einseitig bedruckt werden, sind andere Werte und Prositionen für den Satzspiegel sinvoller.
Beim einseitigen Druck sollte das Seitenverhältniss etwa so sein:
- Kopfsteg und Fußsteg 1 : 2
- Linker Außensteg und rechter Außensteg 1 : 1
Das im Beispielbild gezeigte Verhältniss entspricht bereits dem Standart im europäischer Sprachraum. Bei den Voreinstellungen der LaTeX Standartklassen ist dies nicht so, da diese den Amerikanischen Layouts entsprechen.
Hinweis: Da es bei einem einseitigen Druck wie z.B. einem Aufsatz für die Schule keine Bindung wie bei einem Buch gibt, sollte man hier an die eventuelle Lochung denken und den linken Rand dementsprechend anpassen. Beim anpassen dieses Randes, vl. an die Grösse von "Lochverstärkerringen" denken falls solche eingesetzt werden sollten. Optisch recht schon anzusehen ist wenn rechts neben den Löchern genau so viel Platz wie links zum Blattrand gelassen wird. Bei den Schnellheftern wie sie auch gerne für Bewerbungen verwendet werden sollte unbedingt darauf geachtet werden das keinerlei Text unter der Klemmleiste verschwindet. Zudem möchte ich hier erwähnen das es sich bei einer Bewerbung meist um Einzeldokumente handelt welche aus unterschiedlichem Papier bestehen. Die erste Seite jedes Einzeldokumentes wirkt in der Regel für sich alleine.
Rastersystemverfahren
Ich möchte hier das Rastersystemverfahren zur Bestimmung des idealen Satzspiegels bei einer üblichen DIN A4 Seite zeigen.
Unter einem Rastersystem versteht man ein Ordnungssystem oder auch Gestaltungsraster. Hier durch soll die Vermittlung der einzelnen Informationen verbessert werden.
Satzspiegel erstellen
Beim erstellen des Rasters wird mit dem eigentlichen Satzspiegel begonnen. Dieser darf auf der eigentlichen Seite nicht zu weit oben liegen, da es sonst den Anschein macht der Text würde beim betrachten davon fliegen. Auf der anderen Seite muss man dafür sorgen das der Satzspiegel nicht zu weit unten liegt. Da dies beim Betrachten erdrückend wirkt. Bei den Rändern sollten ästhetisch Proportionen gewählt werden. Wichtig bei Büchern ist das hierbei der Bundsteg nicht auser acht gelassen wird. Da wir für das Binden eines Buches ebenfalls einen entsprechenden Bereich ( Bundsteg ) benötigen, sollte dieser mit eingerechnet werden. Bei einer linken Buchseite haben wir so den Bundsteg auf der rechten Papierseite und bei einer rechten Buchseite befindet sich der Bundsteg auf der linken Papierseite.
Spaltenbreite
Nachdem der Satzspiegel sowei fertiggestellt wurde wird dieser in einzelne Felder bzw. Spalten unterteilt. Wie viele Spalten benötigt werden liegt ganz alleine an der Struckturierung des Satzspiegels und dessen Menge des Inhaltes. Die Spaltenbreite kann also 1, 2, 3 oder 4, 5, 6 und mehr Spalten beinhalten. Je grösser zum Beispiel die Schrift ist welche verwendet wird, desto breite müssen die einzelnen Spalten sein.
Rasterfelder
Nachdem wir die Spalten welche Vertikal sind erzeugt haben, schreiten wir zu den Feldern welche durch horizontallinien hinzugefügt werden. Wie viele Felder man auf diese Art und Weise erstellen möchte liegt einzig und alleine beim Gestalter und sollte von diesem an den einzusetzenden Inhalt angepasst werden.
Schrift
Um die genaue Höhe des Satzspiegels bestimmen zu können, benötigen wir:
- Schriftart
- Schriftgrösse
- Zeilendurchschuss
Ein Zeilendurchschuss bezeichnet den Abstand der Unterlänge eines Kleinbuchstabens, bis zur Oberkante eines darunter angeordneten Großbuchstabens oder Kleinbuchstabens, je nach dem welches höher hinauf ragt.
Der Quellcode zum Beispiel des Zeilendurchschuss:
\begin{document}
\begin{picture}(300,300)
\put(-35.0,20.0){\line(1,0){300}}
\put(-35.0,12.0){\line(1,0){300}}
\put(-38.0,22.0){$ \downarrow $}
\put(-38.0,4.0){$ \uparrow $}
\begin{Huge}
\put(0.0,25.0){Ein Durchschuss Beispiel}
\put(0.0,-5.0){wird hier gezeigt}
\end{Huge}
\end{picture}
\end{document}
Wählen wir nun eine Schriftgrösse von 10pt mit einem Zeilendurchschuss von 3pt kann man zählen wie viele Zeilen in den Seitenspiegel hinein passen. Hier zu muss man allerdings die aller erste Zeile mit der Oberkante des Satzspiegels zueinander ausrichtet. Das heisst eine gemeinsame Bezugslinie finden. Dann werden alle Zeilen welche in unseren Satzspiegel passen abgezählt.
Nun beginnen wir mit dem Rechnen:
Angenommen in unseren Satzspiegel passen 50 Zeilen hinein, so müssen wir von dem Wert 50 einmal 2 abziehen für die Zeilen der Rasterfeldabstände.
( Zeilensumme abzüglich der Rasterfeldabstände ) 50 - 2 = 48
Dies wird nun durch die gewünschte Anzahl der Rasterfelder welche wir haben geteilt.
Bei beispielsweisse 3 Feldern, rechnen wir 48 durch 3
48 : 3 = 16
Ein weiteres Beispiel bei 6 Feldern könnte so aussehen:
50 - 2 = 48 : 6 = 8
Nun fehlen uns noch die Vertikalen Abstande unserer Felder. Dazu müssen wir nun die Unterkante eines unserer Rasterfelder an der Grundlinie der Unterkante ausrichten. Die Oberkante des Feldes wird an die Oberkannte eines Großbuchstabens der benutzten Schrift bündig gesetzt.
9er Rastersystemteilung
Hier ein Beispiel einer Satzspiegelkonstruktion einer neuner Rastersystemteilung. Dieses beispiel wurde von mir unter LaTeX erstellt und deren Quellcode steht direkt unter der Abbildung.
Diese Seite wurde horizontal u. vertikal in die gleiche Anzahl von Rasterfeldern aufgeteilt. Am inneren u. oberen Rand bleiben jeweils ein Rasterfeld frei, am äusseren und unteren jeweils zwei.
Hier der dazugehörige Quellcode:
\begin{document}
\begin{center}
\begin{picture}(583,841)
\put(65.0,-3.0){\line(0,1){845}}
\put(131.0,-3.0){\line(0,1){845}}
\put(195.0,-3.0){\line(0,1){845}}
\put(259.0,-3.0){\line(0,1){845}}
\put(323,-3.0){\line(0,1){845}}
\put(387,-3.0){\line(0,1){845}}
\put(451,-3.0){\line(0,1){845}}
\put(515,-3.0){\line(0,1){845}}
\put(-7.0,93.0){\line(1,0){598}}
\put(-6.0,187.0){\line(1,0){598}}
\put(-6.0,280.0){\line(1,0){598}}
\put(-6.0,373){\line(1,0){598}}
\put(-6.0,466.0){\line(1,0){598}}
\put(-6.0,559.0){\line(1,0){598}}
\put(-6.0,652.0){\line(1,0){598}}
\put(-6.0,745.0){\line(1,0){598}}
\put(65.0,186.0){\line(1,0){386}}
\put(65.0,744.0){\line(1,0){386}}
\put(64.0,186.0){\line(0,1){558}}
\put(450.0,186.0){\line(0,1){558}}
\end{picture}
\end{center}
\end{document}
Goldener Schnitt
Der Goldene Schnitt spielt beim Satzspiegel eine grosse Rolle, da dieser in seiner Art sehr harmonisch ist. Das wohl beste Beispiel für den Goldenen Schnitt ist die original Gutenberg Bibel. Gutenberg selbst, teilte bereits das Papier nach dem Goldenen Schnitt. Desweiteren findet man die Harmonische Einteilung vom Goldenen Schnitt in der freien Natur wie beispielsweise beim Schachtelhalm und Eichenblatt. Genauso in der Kunst und Architektur.
Hier ein einfaches Beispiel für einen Goldenen Schnitt:
Der Quellcode zur Zeichnung:
\begin{document}
\begin{picture}(300,300)
\put(-35.0,60.0){\line(1,0){150}}
\put(-35.0,60.0){\circle*{5.0}}
\put(115.0,60.0){\circle*{5.0}}
\put(37.0,70.0){a}
\put(-35.0,20.0){\line(1,0){150}}
\put(-35.0,20.0){\circle*{5.0}}
\put(115.0,20.0){\circle*{5.0}}
\put(55.0,20.0){\circle*{5.0}}
\put(7.0,30.0){b}
\put(83.0,30.0){c}
\end{picture}
\end{document}
- a = b + c
Die Länge (c) muss sich zur Länge (b) so verhalten wie die Länge (b) zur Länge (a).
Mathematisch gesehen bezeichnet der Goldene Schnitt also ein Teilungsverhältnis. Hierbei wird also eine Strecke namens (a) zuerst in zwei weitere Teile unterteilt. So das sich die größere Teilstrecke (b) proportional zur Gesamtstrecke verhält wie die kleinere Teilstrecke (c) zu der größeren Teilstrecke (b).
Wieso nun der Goldene Schnitt ?
Nun, das menschliche Auge sieht eine Fläche welche im Verhältnis 3:5 oder 2:3 ist sehr harmonisch. Genau genommen 1 : 1,618.
Bereits die Griechen hatten herraus gefunden das auch in den einzelnen Proportionen des menschlichen Körpers sich genau dieses Teilungsverhältnis wiederfindet. Dies ist auch ein weiterer Grund weshalb wir genau dieses Teilungsverhältnis so angenehm empfinden.
Der Goldene Schnitt besagt also das sich der Satzspiegel nicht genau in der mitte des Blattes befinden soll. Sondern mehr nach links oder rechts außen oder mehr ins obere des Blattes, da hierdurch mehr Spannung entsteht als wenn der Satzspiegel genau in der Mitte wäre.
Ich bin mir sicher das nun jeder weis was damit gemeint ist, man kennt es zum Beispiel auch von der Fotografie. Hierbei wird genauso bei der Bildgestaltung versucht ein Objekt nicht genau in die Mitte des Bildes zu setzen da wir so nicht wirklich Spannung in das Bild hineinbringen können.
Darstellungsbeispiel
Satzspiegelkonstruktion einer Doppelseite nach dem Goldenen Schnitt:
- Abb. 1: Die Diagonalen werden über die Doppelseite konstruiert und die Einzelnseiten zeigen ebenfalls die Diagonalen von oben innen, nach unten aussen.
- Abb. 2: Die oberen Ecken des Rechtecks, die unteren äusseren Ecken liegen auf den konstruierten Diagonalen. Desto weiter oben u. außen die obere innere Ecke gewählt werden, desto größer wird der Satzspiegel und umso kleiner werden die Papierränder.
- Abb. 3: Satzspiegel im Verhältnis des Goldenen Schnittes.
Welches Konstruktionsverfahren
Wir haben nun gelernt was ein Satzspiegel ist und wozu dieser benötigt wird. Welches Verfahren man nun zur generierung des Satzspiegels verwendet bleibt jedem selbst überlassen. Vielen gefällt zum Beispiel bei einem Satzspiegel welcher mit dem Goldenen Schnitt erstellt wurde nicht das dieser bei einer Doppelseite so weit oben am Kopfsteg und am linken/rechten Außensteg liegt. Am Ende ist alles eine reine Geschmacksache die vom Gestalter dementsprechend gewählt wird.
Satzspiegel der Standartklassen
Wenn wir mit LaTeX unsere Dokumente erstellen, wundern wir uns doch des öffteren über die recht breiten Außenstege bzw. Seitenränder. Als erstes muss hier erwähnt werden, ( dies ist richtig und absolut korrekt ) so wie es ist. Wir selbst sind es einfach nur gewohnt Seitenlayouts anzusehen mit wesentlich geringeren Seitenrändern da dies bei uns hier in der Union ( europäischer Sprachraum ) so üblich ist. Die LaTeX Standartdokumentenklassen verwenden oder halten sich hier an die amerikanische Layouts.
Bei der Auswahl einer der entsprechenden Standartklassen unter LaTeX wird zudem auch der Satzspiegel und weiteres wie beispielsweisse die Außenstege / Seitenränder etc. festgelegt.
Hier zuerst eine Auswahl der Klassenoptionen des Seitenlayoutes, da sich bei der Wahl dieser auch zudem zahlreiche andere Dinge wie u.a. auch der Satzspiegel in seiner Aufteilung etc. verändert.
Bei uns übliche Grössen ( EU )
- a4paper = 210 × 297 mm ( Viertelbogen - Briefpapier, Formulare, Hefte, Zeitschriften, Kataloge )
- a5paper = 148 × 210 mm ( Blatt - Notizblöcke, Schulhefte )
- b5paper = 176 × 250 mm ( Bücher )
Bei uns nicht übliche Grössen ( US )
- letterpaper = 8 1/2 × 11 Zoll
- legalpaper = 8 1/2 × 14 Zoll
- executivepaper = 7 1/4 × 10 1/2 Zoll
Wer mit der Gestaltung bei Verwendung der Standartklassen so nicht zu frieden ist, kann hier auch selbst Hand anlegen. Mit Hilfe der Dimensionsparameter auf welche wir gleich näher eingehen werden können so zahlreiche Parameter verändert werden.
ISO Papier Formate
Eben wurden ein paar Papierformate aufgelistet, für ein besseres Verständniss habe hier ich eine kleine Grafik angefertigt um die entsprechenden Grössenunterschiede besser wahr zu nehmen.
Tabellarische Übersicht
| DIN-A | DIN-B | DIN-C | DIN-D | DIN-E | |
|---|---|---|---|---|---|
| 1 | 594 × 841 | 707 × 1000 | 648 × 917 | 545 × 771 | 560 × 800 |
| 2 | 420 × 594 | 500 × 707 | 458 × 648 | 385 × 545 | 400 × 560 |
| 3 | 297 × 420 | 353 × 500 | 324 × 458 | 272 × 385 | 280 × 400 |
| 4 | 210 × 297 | 250 × 353 | 229 × 324 | 192 × 272 | 200 × 280 |
| 5 | 148 × 210 | 176 × 250 | 162 × 229 | 136 × 192 | 140 × 200 |
| 6 | 105 × 148 | 125 × 176 | 114 × 162 | 96 × 136 | 100 × 140 |
| 7 | 74 × 105 | 88 × 125 | 81 × 114 | 68 × 96 | 70 × 100 |
| 8 | 52 × 74 | 62 × 88 | 57 × 81 | ||
| 9 | 37 × 52 | 44 × 62 | 40 × 57 | ||
| 10 | 26 × 37 | 31 × 44 | 28 × 40 |
Dimensionsparamter
Mit unseren Dimensionsparametern ist es möglich, sämtliche für die Darstellung benötigte Werte zu ändern. Dies können Seitenränder, Abstände von Kopf und Fuß etc. sein.
Höhe Satzspiegel
\setlength{\textheight}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hierdurch wird die Höhe des Satzspiegels bestimmt. Die Höhe ist zwischen Kopf und Fußbereich in denen zum Beispiel auch der tote Kolumnentitel steht. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Breite Satzspiegel
\setlength{\textwidth}{220mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hierdurch wird die Breite des Satzspiegels bestimmt. Dies ist der Bereich in welchem unser eigentlich Text steht. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Kopfsteg
\setlength{\topmargin}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Er setzt den Abstand zwischen unserem oberen Blattrand und dem Seitenkopf. Der Seitenkopf ist der Bereich in welchem auch unser tote Kolumnentitel stehen kann. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Linker Rand Einseitig
\setlength{\oddsidemargin}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Er setzt die Breite des Aussensteges, dies ist der Bereich vom linken Blattrand bis hin zum Satzspiegel. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Linker Rand Zweiseitig
\setlength{\evensidemargin}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Wird ein zweiseitiges Dokument erstellt, so wird hier der Wert des linken Randes vom rechten Blatt eingestellt. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenkopf zum Satzspiegel
\setlength{\headsep}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hier wird der Abstand zwischen dem Seitenkopf und dem Satzspiegel bestimmt. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenkopfbereich
\setlength{\headheight}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Mit diesem Befehl wird die Höhe angegeben des Bereiches welcher für den Seitenkopf reserviert wird. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenfuß zum Satzspiegel
\setlength{\footskip}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Legt den Abstand des Seitenfußes bis zum Satzspiegel fest. Im Seitenfuß kann zum Beispiel ein toter Kolumnentitel stehen. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenfußbereich
\setlength{\footheight}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hier wird die Höhe des Bereiches bestimmt welcher für den Seitenfuß reserviert wird. Gleich wie beim Seitenkopfbereich. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Marginalie zum Satzspiegel
\setlength{\marginparsep}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Mit diesem Befehl legen wir den Abstand zwischen unserem Satzspiegel und einer Marginalie fest. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Marginalie Breite
\setlength{\marginparwidth}{10mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Wir können hiermit die Breite des für eine Marginalie bestimmten Bereiches festlegen. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Marginalie zur Randnotiz
\setlength{\marginparpush}{30mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hier können wir den mindest Abstand angeben welcher vertikel zwischen mehreren Marginalie sein soll. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Abstand zwischen Absatz
\setlength{\parskip}{5mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. So wird der Abstand zwischen mehreren aufeinandervollgenden Absätzen angegeben. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Zeilendurchschuss
\setlength{\baselineskip}{12pt}
Der Zeilendurchschuss kann hiermit beeinflusst werden. Man verwendet i.d.R ca. 20% bis 30% der Schriftgrösse. D.h. bei einer 10pt grossen Schrift, sollte der Durchschuss ca. 12pt bis 13pt betragen.
Darstellungsbeispiele
Für ein besseres Verstehen habe ich das ganze mal grafisch versucht darzustellen. Der Quellcode ist wie immer unterhalb des Bildes zu finden.
Hier der dazugehörige Quellcode:
\begin{document}
\fbox{
\begin{picture}(331,594)
\put(-6.0,610.0){\line(0,1){10.0}}
\put(337.0,610.0){\line(0,1){10.0}}
\put(122.0,610.0){Kolumnentitel tot}
\put(80.0,610.0){$ \leftarrow $}
\put(40.0,610.0){$ \leftarrow $}
\put(240.0,610.0){$ \rightarrow $}
\put(280.0,610.0){$ \rightarrow $}
\put(0.0,575.0){Kolumnentitel lebend}
\put(+278.0,575.0){Paginierung}
\put(-6.0,560.0){\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots\dots}
\put(143.0,330.0){textheight}
\put(100.0,300.0){textwidth}
\put(80.0,300.0){$ \leftarrow $}
\put(162.0,350.0){$ \uparrow $}
\put(162.0,250.0){$ \downarrow $}
\put(240.0,300.0){$ \rightarrow $}
\put(-6.0,-20.0){\line(0,1){10.0}}
\put(337.0,-20.0){\line(0,1){10.0}}
\put(122.0,-20.0){Kolumnentitel tot}
\put(80.0,-20.0){$ \leftarrow $}
\put(40.0,-20.0){$ \leftarrow $}
\put(240.0,-20.0){$ \rightarrow $}
\put(280.0,-20.0){$ \rightarrow $}
\put(-80.0,300.0){oddsidemargin}
\put(-84.0,310.0){$ \leftarrow $}
\put(-22.0,290.0){$ \rightarrow $}
\put(398.0,300.0){Aussensteg}
\put(375.0,300.0){$ \leftarrow $}
\put(459.0,300.0){$ \rightarrow $}
\put(-55.0,-3.0){\line(1,0){10.0}}
\put(-65.0,-80.0){Fusssteg}
\put(-77.0,-90.0){Unterer Rand}
\put(-52.0,-55.0){$ \uparrow $}
\put(-52.0,-115.0){$ \downarrow $}
\put(-55.0,620.0){\line(1,0){10.0}}
\put(385.0,601.0){headsep}
\put(373.0,590.0){$ \uparrow $}
\put(373.0,612.0){$ \downarrow $}
\put(370.0,600.0){\line(1,0){10.0}}
\put(370.0,608.0){\line(1,0){10.0}}
\put(430.0,618.0){\line(1,0){10.0}}
\put(430.0,608.0){\line(1,0){10.0}}
\put(445.0,609.0){headheight}
\put(433.0,598.0){$ \uparrow $}
\put(433.0,622.0){$ \downarrow $}
\put(-65.0,666.0){topmargin}
\put(-52.0,685.0){$ \uparrow $}
\put(-52.0,647.0){$ \downarrow $}
\put(359.0,450.0){marginparsep}
\put(343.0,450.0){$ \leftarrow $}
\put(422.0,450.0){$ \rightarrow $}
\put(440.0,448.0){\line(0,1){10.0}}
\put(359.0,520.0){marginparwidth}
\put(348.0,520.0){$ \leftarrow $}
\put(429.0,520.0){$ \rightarrow $}
\put(440.0,518.0){\line(0,1){10.0}}
\put(347.0,518.0){\line(0,1){10.0}}
\put(359.0,482.0){marginparpush}
\put(347.0,482.0){$ \uparrow $}
\put(430.0,482.0){$ \downarrow $}
\put(385.0,-15.0){footskip}
\put(373.0,-29.0){$ \uparrow $}
\put(373.0,1.0){$ \downarrow $}
\put(370.0,-20.0){\line(1,0){10.0}}
\put(370.0,-3.0){\line(1,0){10.0}}
\put(445.0,-19.0){footheight}
\put(433.0,-29.0){$ \uparrow $}
\put(433.0,-6.0){$ \downarrow $}
\put(430.0,-20.0){\line(1,0){10.0}}
\put(430.0,-10.0){\line(1,0){10.0}}
\end{picture}
}
\end{document}
Marginalien Seite
Was Marginalien sind wurde ja bereits weiter oben beschrieben. Was uns nun noch fehlt ist die Möglichkeit die Marginalien in den anderen Seiten steg schreiben zu lassen, falls den dies gewünscht wäre.
Marginalien Rechts
Mit dem hier gezeigten Beispiel werden die Marginalien bei einem einseitigen Dokument in den rechten Ausensteg geschrieben.
\begin{document}
\marginpar{Rechts}
\end{document}
Marginalien Links
Mit dem hier gezeigten Beispiel und der Verwendung von reversemarginpar werden die Marginalien bei einem einseitigen Dokument in den linken Ausensteg geschrieben.
\begin{document}
\reversemarginpar
\marginpar{Links}
\end{document}
Marginalien bei Doppelseite
Bei der Verwendung von Doppelseiten werden die Marginalien immer in den Außensteg geschrieben. D.h. wenn ich in meiner Präambel twoside mit aufgenommen habe wie es beispielsweisse bei "Book" der Standart ist, so werden auf der ersten rechten Seite des Dokumentes doe Marginalien in den rechten Außensteg geschrieben und auf der Seite 2 d.h. der Rückseite der ersten Seite in den linken Außensteg. Somit sind die Marginalien immer im Außensteg vorhanden.
So kann zum Beispiel der twoside Eintrag in der Präambel aussehen.
\documentclass[a4paper,twoside,10pt]{article}
Die Marginalien werden bei der Verwendung von twoside weiterhin ganz normal mit dem Befehl \marginpar geschrieben.
Layout Vergleich
Da hier nun bereits öffter erwähnt wurde das es kleine Unterschiede bei den Layouts gibt, möchte ich diese gerne grafisch für ein besseres Verständniss darstellen:
Druck einseitig - US / EU Layout
Einseitig direkter Vergleich
Im direkten Vergleich ist der Grossenunterschied des Satzspiegels deutlich zu sehen. Beim EU Layout ist der Satzspiegel etwas breiter und der untere Fußsteg grösser als der Kopfsteg. Beim US Layout ist der gesamte Satzspiegel etwas schmaler, dafür sind die Stege oben/unten rechts/links gleich.
Druck beidseitig - US / EU Layout
Hier noch ein weiteres Beispiel für den beidseitigen Druck wie bei Büchern etc.
Beidseitig direkter Vergleich
Auch hier sind wieder im direkten Vergleich die Unterschiede von Höhe/Breite sowie den Stegen gut zu erkennen.
Automatische Satzspiegelkonstruktion
Wem also die amerikanischen LaTeX Standartlayouts nicht gefallen, kann diese mit den oben beschriebenden Dimensionsparamtern dementsprechend ändern. Da das ändern der gesamten Parameter eine knifflige Arbeit ist bei der das entsprechende Ergebniss am Ende dann doch nicht immer den eigenen Vorstellungen entspricht, gibt es eine einfachere Lösung die den Satzspiegel selbst berechnet und an die richtige Stelle platzieren zu lassen.
Das Zauberpacket nennt sich Typearea und stammt aus KOMA-Script.
KOMA-Script ist eine Sammlung von Dokumentenklassen ähnlich wie article, book usw. welche aber an den europäischen Raum und dessen Standarts angepasst wurden. Zu dieser Anpassung trägt typearea.sty seinen Teil bei, indem von ihm der Satzspiegel berechnet und dessen Prosition dementsprechend bestimmt wird. Somit fällt die ganze Handarbeit wie weiter oben beschrieben "festlegen der Abstände etc." weg. Typearea ist zwar bei den Standartklassen von LaTeX nicht dabei, kann aber dennoch bei ihrer Verwendung genutzt werden. D.h. nach der Installation von KOMA-Script oder Typearea müssen nicht unbedingt die KOMA-Script Klassen verwendet werden da typearea.sty auch in die Standartklassen mit als usepackage eingebunden werden kann.
Faktoren
Für die automatische erstellung kommen verschiedene Faktoren zusammen:
- Schriftgrösse
- Laufweite
- Schriftart
- Durchschuss
- Platz
- Wortlänge
Wichtig bei der Schrift ist ob diese eine Serifenlose Schrift oder eine Schrift mit Serifen ist, da durch Serifen die Zeilenwirkung verstärkt wird. Somit ist es für unser Auge einfacher den Wortern und Zeilen beim lesen besser zu vollgen. Fazit wäre das eine Zeile mit einer Serifenschrift somit länger sein dürfte als eine Zeile die mit Serifenloser Schrift geschrieben.
Beim Durchschuss ist es so, das hier ein etwas grösserer das lesen wesentlich erleichtern kann. Ein zu gross gewählter erschwärt es dagegen. Schaut man sich eine Seite mit zu grossem Durchschuss an, fällt auf das die Grauwerte gestört sind. In der Regel ist der LaTeX Standart so eingestellt das wir mit ca. 20% Durchschuss arbeiten.
Bei der Zeilenlänge kommt es ganz darauf an. Wenn wir alles in allem rechnen, d.h. mit Leerzeichen etc. kommen wir mit 60 bis 70 Zeichen pro Zeile auf einen recht guten Mittelwert.
Anwendung
Um Typearea verwenden zu können, benötigen wir einen kleinen Eintrag in unserer Präambel:
\usepackage[...]{typearea}
Hierbei müssen wir allerdings noch einen oder mehrere weitere Werte [...] Setzen welche im Anschluss kurz beschrieben werden.
BCOR - Wert
Der in obigem Beispiel noch fehlende Wert kann zum einen der BCOR Wert sein. Der BCOR Wert ist für die Bindekorrektur welche eventuell benötigt wird. Die Bindekorrektur benötigen wir da bei einer Bindung ein kleiner Teil unseres Steges ( Bundsteg ) verlohren geht und somit die Stege nicht mehr stimmen würden.
Ein Beispiel für eine Bindekorrektur kann so aussehen:
\usepackage[BCOR8.25mm]{typearea}
Was noch erwähnenswert bei der Bindekorrektur ist, das man pro Blatt ca. 0,75 mm zur Bindekorrektur dazu rechnen sollte, da beim Umschlagen einer Seite wenn diese zum Beispiel in einem Schnellhefter abgeheftet wurde durch den Falz oder Knick dieser Wert verlohren geht.
Wird auf eine Bindekorrektur verzichtet, so kann dieser Eintrag vollgendermassen aussehen:
\usepackage[BCOR0pt]{typearea}
DIV - Wert
Den DIV Faktor Wert benötigen wir um anzugeben in wie viele Streifen wir unsere Seite horizontal und vertikel für die Satzspiegelberechnung unterteilen möchten. Weiter oben haben wir ein Beispiel eines 9ner Rastersystemes gezeigt. Hier wäre für dieses Rastersystem [DIV9] richtig.
Da es zum grössten Teil auf die verwendete Schriftgrösse ankommen, so gibt es hier zu empfehlende Werte die ich keinem vorenthalten möchte.
Empfohlene Werte
Für DIN A4 bei einer Grundschriftgrösse:
- 10 pt = 8 DIV
- 11 pt = 10 DIV
- 12 pt = 12 DIV
In unserer Präambel könnte ein Eintrag so aussehen:
\usepackage[DIV8]{typearea}
Neuberechnung
Desweiteren haben wir sogar die Möglichkeit uns unseren Satzspiegel von Typearea ohne eine expliziete DIV Faktor Angabe berechnen zu lassen. Es wird also ein Satzspiegel mit einem guten DIV Wert berechnet. Für eine solche Berechnung verwenden wir vollgeden Eintrag in unserer Präambel:
\usepackage[DIVcalc]{typearea}
Möchte man wissen welcher als optimaler DIV Wert bei der Verwendung von Calc verwendet wurde, so reicht hier ein kleiner Blick in unsere *.log Datei. Hier sollte dann ein ähnlich wie hier gezeigter Eintrag zu finden sein:
DIV calculation for typearea with good linewidth. Package typearea Info: These are the values describing the layout: (typearea) DIV = 7
Mittelalterliche Kreisberechnung
Wir können uns den Satzspiegel sogar nach der mittelalterlichen Kreisberechnung von Typearea berechnen lassen:
\usepackage[DIVclassic]{typearea}
Anwendungsbeispiel
Hier nun ein vollständiges Anwendungsbeispiel:
\usepackage[BCOR12mm,DIV8]{typearea}
Satzspiegelmasse Übersicht
Für die entsprechenden DIV Werte die anzugeben sind, sind entsprechende Voreinstellungen für den Satzspiegel Stege etc. vorhanden.
Kleine Übersicht:
| DIV-Wert | Satzspiegel Breite | Satzspiegel Höhe | Kopfsteg | Außensteg | |
|---|---|---|---|---|---|
| 6 | 105,00 | 148,50 | 49,50 | 35,00 | |
| 7 | 120,00 | 169,71 | 42,43 | 30,00 | |
| 8 | 131,25 | 185,63 | 37,13 | 26,25 | |
| 9 | 140,00 | 198,00 | 33,00 | 23,33 | |
| 10 | 147,00 | 207,90 | 29,70 | 21,00 | |
| 11 | 152,73 | 216,00 | 27,00 | 19,09 | |
| 12 | 157,50 | 222,75 | 24,75 | 17,50 | |
| 13 | 161,54 | 228,46 | 22,85 | 16,15 | |
| 14 | 165,00 | 233,36 | 21,21 | 15,00 | |
| 15 | 168,00 | 237,60 | 19,80 | 14,00 |
Hierbei ist allerding zu sagen, das keine Bindekorrekturen verwendet wurden.
Die Werte in der hier dargestellten Tabelle, stammen aus "Die Anleitung - KOMA Script" welches auch unter Distributionen & Links hier im LaTeX Wiki Book aufgelistet und verlinkt ist.
Schriften
Bevor wir uns daran machen mit weiteren Schriften zu arbeiten als die welche uns unter LaTeX standartmäßig zu verfügung seteh, sollten wir uns ein bisschen Grundwissen über Schrift und Schriften aneignen.
Schriftbaum & Analyse
Bei uns hier im deutschen Kreis unterschieden wir hauptsächlich zwischen zwei Schriftarten:
- Gebrochene Schrift - ( Auch Fraktur genannt, allerdings nicht richtig )
- Antigua Schrift
Gebrochene Schrift
Die gebrochene Schrift wird auch oft als Fraktur bezeichnet was allerdings so nicht richtig ist. Der Begrif Gebrochene Schrift bezeichnet eine latainische Schrift bei der die Bögen der Schrift aus einer einzigen Schreibbewegung sind. Zudem sind bei der gebrochenen Schrift die einzelnen Bögen in den Buchstaben gebrochen was heissen soll das ein Richtungswechsel der Strichführung innerhalb eines Bogens vorhanden ist.
Bekannte gebrochene Schriften sind beispielsweisse:
- Schwabacher
- Initale
- Rotunda
Die Gebrochenen Schriften werden in weitere fünf Gruppen unterteilt laut DIN16518 welche insgesamt 14 Gruppen einteilt:
- Schwabacher
- Gotisch (Textura)
- Rundgotisch (Rotunda)
- Fraktur
- Fraktur-Varianten
Die anderen neun fehlenden Gruppen sind zum Teil sonstige oder auch andere welche zur Antigua gehören.
Antigua Schrift
Als Antigua wird eine Schriftart bezeichnet bei der die Bögen der einzelnen Buchstaben aus einem einzigen Schriftzug entstanden sind. Diese Bögen beinhalten keine Richtungsänderungen oder Richtungswechsel der Schreibform wie es etwa bei den Gebrochenen Schriften zu sehen ist. In der Westlichen Sprache sind die Antigua die wohl am meisten verwendete Druck- und Schreibschriften. So wie die Gebrochenen Schriften werden auch die Antigua in weitere Gruppen unterteilt.
- Venezianische Renaissance-Antiqua
- Französische Renaissance-Antiqua
- Barock-Antiqua
- Klassizistische Antiqua
- Serifenbetonte Linear-Antiqua
- Serifenlose Linear-Antiqua
- Antiqua-Varianten
- Schreibschriften
- Handschriftliche Antiqua
Serifen
Desweiteren wird unterschieden in Schriften mit und in Schriften ohne Serifen. Eine Serife ist ein Strich bei einem Buchstaben der quer zu seiner Grundline abschliesst. Durch diese kleinen Serifen bei den einzelnen Buchstaben wirkt der damit geschriebene Text so das es unserem Auge beim lesen leichter fällt der Linie bzw. Zeile welche wir gerade lesen zu vollgen. Wenn eine Serifen Schrift verwendet wird, kann die eigentliche Zeilenlänge mit ihrer Zeichenanzahl etwas länger sein. Sollte aber dennoch nicht über 70 Zeichen kommen. Alle Zeilen mit mehr als 70 Zeichen einschliesslich den Leerzeichen sind selbst für geübte leser nicht mehr angenehm zu lesen. Serfien sind durch die betonung der Grundlinie sowie der Mitellinie besonders bei grösseren Texten geeignet.
Grund- und Mittellinie
Zur besseren Verdeutlichung hier eine Abbildung welche die Grund- und Mittellinie zeigt.
Quellcode:
\begin{document}
\begin{picture}(300,300)
\put(-35.0,36.0){\line(1,0){250}}
\put(-35.0,25.0){\line(1,0){250}}
\put(-38.0,38.0){$ \downarrow $}
\begin{scriptsize}
\put(-37.0,46.0){Mittellinie}
\end{scriptsize}
\put(-38.0,18.0){$ \uparrow $}
\begin{scriptsize}
\put(-37.0,10.0){Grundlinie}
\end{scriptsize}
\begin{Huge}
\put(0.0,25.0){Super Linux Club}
\end{Huge}
\end{picture}
\end{document}
Schriftfamilie
Unter dem Namen Schriftfamilie verseht man alle Varianten eines Schriftbildes einer Schrift. Eine Schriftfamilie wäre beispielsweisse Computer Modern Roman da diese weitere Schriftschnitte enthält.
Schriftschnitte
Als Schriftschnitt wird auch der Schriftstiel bezeichnet. Dieser enthält verschiedene Varianten einer Schriftfamilie wie zum Beispiel:
- Schriftstärke
- Schriftdicke
- Schriftlage
Als dekoratieve Schriftschnitte könne auch:
- Kapitälchen
- Initalen
- Mediävalziffern
- Bruchziffern
- Ligaturen
zählen.
Schriftgrad
Als Schriftgrad wird auch das Schriftsatzmaß bezeichnet das in weitere Punkte unterteilt wird.
- Konsultationsgröße
- Lesegröße
- Schaugröße
Konsultationsgröße
Als Konsulationsgröße wird eine Schrift mit 3 bis 9 Didot-Punkten bezeichnet.
Lesegröße
Als Lesegröße wird eine Schrift mit 10 bis 13 Didot-Punkten bezeichnet. Daher wird bei den meisten texten diese als Ideale Grundschriftgröße gesehen.
Schaugröße
Als Schaugröße wird eine Schrift mit 14 bis 47 Didot-Punkten bezeichnet
Schriftgrad - Fußnoten & Marginalien
Der Schriftgrad von Fußnoten und Marginalien ist in der Regel 2 bis 5 Didot-Punkte kleiner als die Grundschrift. Wird also eine Grundschrift von 10 Didot-Punkten verwendet, so haben die Fußnoten, Marginalien eine Größe von 5 bis 8 Didot-Punkten.
Schrift Qualität
In der EDV werden verschiedene Schriften in unterschiedlichen Dateiformaten zu verfügung gestellt. Die zwei bekanntesten und auch weit verbreitetsten sind die TrueType Schriften und die welche im PostScript Format vorliegen. Vorgestellt wurde TrueType im Jahr 1991 von der Firma Apple Inc. und lizenziert von Microsoft Corporation. Integriert sind diese in den Betriebsystemen Windows und MacOS. Unter Linux und anderen Unix Systemen ist es unter FreeType verfügbar.
Die TrueType Schriften werden mit dem selben Prinzip wie die Vektorgrafiken aufgebaut, d.h. aus Konturen.
PostScript wird seit 1984 von Adobe entwikelt und unterscheidet sich am stärksten von den TrueType Schriften in den Kurven.
Bei TrueType Schriften werden Bézierkurven der zweiten Ordnung verwendet, bei PostScript Schriften Bézierkurven der dritten Ordnung. Hier durch ist die Qualität der PostScript Schriften im allgemeinen höher als die der TrueType Schriften.
Weitere Schriften
Unter LaTeX haben wir die Möglichkeit viele weitere Schriften verwenden zu können, ich möchte zeigen wie es geht. Zu aller erst, ist es wichtig zu sagen das die Art und Weise die wir bereits in den Grundlagen kennengelernt haben um eine Schrift auszuwählen hier etwas anderst funktioniert. Wir haben ein paar Punkte die ich kurz nennen möchte, da diese für die Auswahl oder Bestimmung unserer gewünschten Schrift benötigt werden.
Schriftatribute:
- Fontencoding
- Fontfamily
- Fontseries
- Fontshape
- Fontsize
Fontencoding: Hiermit wird der gewünschte Zeichensatz angegeben.
Fontfamily: Damit wird unsere Schriftfamilie ausgewählt.
Fontseries: Wird für die Schriftstärke benötigt.
Fontshape: Benötigen wir um zu bestimmen ob wir eine aufrechte oder geneigte Form möchten.
Fontsize: Dint zur Grössenbestimmung der Schrift und dessen Zeilenabstand oder Durchschuss.
Sehr wichtig zu erwähnen ist hier das man eventuell diverse Pakete mit weiteren Schriften installieren muss um diese nutzen zu können. Dazu kommt nocht das nicht immer alle Schriften in allen Grössen etc. verfügbar sein können.
Fontencoding - Zeichensatz
Mit Zeichensatz wird eine Sammlung von diversen Zeichen bezeichnet. Dies können Buchstaben wie auch Mathematische oder Sonderzeichen sein.
Fontfamily - Schriftfamilie
Unter der Bezeichnung Schriftfamilie versteht man eine Gruppe von Schriftstielen welche gemeinsame Merkmale in ihrer Form aufweissen. Eine Schriftfamilie kann also aus vielen einzelnen Schriften bestehen, welche wiederum als Schriftfamilie in verschiedene Klassifikationen oder auch Schriftsippen als Familie zugeordnet werden können. Eine unter LaTeX verfügbare Schriftfamilie wäre beispielsweisse die Computer Modern Roman.
Fontseries - Schriftstärke
Mit der Schriftstärke wird die Dicke der Schrift oder deren Stärke, Fette bezeichnet. Die genaue Bezeichnung der Schrift, ob diese nun dick oder nicht ist steht dem Hersteller der Schrift frei. Leider funktioniert hirdurch die Einteilung in die Schriftstärkenklassen nicht so gut wie man es gerne hätte, da all dies eine reine Geschmacksache ist. Sehr oft werden hier die Bezeichnungen durcheinander geworfen so das Schriften mit der gleichen Stärke unterschiedlich zugeordnet und benannt werden.
Schriftstärken
- Ultraleicht = Ultra Light, Ultra Thin
- Extraleicht = Extra Light, Fein, Thin
- Leicht = Light, Light Plain
- Halbleicht = Semi Light, Mager, Semi Light Plain
- Normal = Regular, Buch, Werk, Book, Medium, Plain, Roman
- Halbfett = Semi Bold, Kräftig)
- Fett = Bold, Dreiviertelfett, Demi, Heavy
- Extrafett = Extra Bold, Black
- Ultrafett = Ultra Bold, Extra Black, Ultra
Schriftdicke
Unter der Schriftdicke versteht man die Breite der Buchstaben.
- Ultraschmal = Ultra Condensed
- Extraschmal = Extra Condensed
- Schmal = Condensed, Compressed, Narrow
- Halbschmal =Semi Condensed
- Normal = Regular
- Halbbreit = Semi Expanded
- Breit = Expanded, Extended)
- Extrabreit = Extra Expanded
- Ultrabreit = Ultra Expanded
Fontshape - Schriftlage
Mit Schriftlage geben wir an ob wir eine Kursive, Schräggestellte oder Aufrechte Schrift möchten.
Schriftlage
- Normal = Aufrecht, upright
- Kursiv
- Italic, oblique = Echte Kursive
- slanted, sloped roman = Unechte Kursive
- Echte Kursive = Hier wurde die Schrift vom Desinger entworfen.
- Unechte Kursive = Die Schrift wurde mit Hilfe von Software einfach schräg gestellt.
Fontsize - Schriftgrösse
Unter Fontsize versteht man die Schriftgrösse welche in der Regel in (pt) = Punktgrösse angegeben ist. Eine 12pt Schrift ist in etwa das was man von einer Schreibmaschiene her kennt.
In der Regel stehen einem vollgende Grössen zu verfügung:
5, 6, 7, 8, 9, 10, 10.95, 12, 14.4, 17.28, 20.48, 24.88
Desweiteren kann mit dem Befehl für die Schriftgrösse zudem der Zeilenabstand ( Durchschuss ) in (pt) Punktgrösse mit angegeben werden.
Schriften Installieren
Um unter LaTeX weitere Schriften verwenden zu können, müssen diese erst installiert werden. Für die Installation sollte man zuerst schauen ob nicht vl. der Distributor bereits fertige Binäre Pakete zur Installation für seine jeweilige Distribution anbietet welche weitere Schriften für LaTeX enthalten. Da ich selbst nicht jede Distribution kenne und im Einsatz habe, kann ich hier nur einen einfachen weg zeigen um unter meiner verwendeten Distribution weitere Schriften zu installieren.
Tipp: Debian
Stand: 07/2007
Unter Debian gibt es derzeit das Paket texlive-fonts-extra für das TexLive System welches weitere Schriften etc. enthällt.
Ansonsten besteht die Möglichkeit sich die einzelnen dementsprechenden Pakete bei CTAN zu besorgen.
Für deren Installation sollte man die jeweils zugehörige Hilfedateien lesen.
Im Anschluss wird hier nun beschrieben wie den eine Installierte Schrift unter LaTeX verwendet werden kann.
Schriften Laden
Wenn weitere Schriften installiert wurden, müssen wir diese zuerst auswählen um sie verwenden zu können. Zum einen kann es nötig sein das vor der Verwendung erst ein weiteres Paket mit in die Präambel geschrieben werden muss um dieses laden zu können. Eine Sehr bekannte Schrift wäre beispielsweisse die Schwabacher Schrift. Soll diese nach deren Installation unter LaTeX in einem Dokument verwendet werden, muss sie zuvor als Paket mit in die Präambel geschrieben werden. Hier ein Beispiel dazu:
\usepackage{oldgerm}
Welcher Style Name in diesem Fall oldgerm mit in die Präambel zu schreiben ist, muss der dazugehörigen Dokumentation des installierten Paketes entnommen werden.
Schrift Auswählen
Haben wir den entsprechenden Befehl in unsere Präambel für das laden des Paketes geschrieben, so können wir unsere neue Schrift schliesslich verwenden. Was uns nun noch fehlt ist die genaue Angabe was wir den überhaupt verwenden wollen. Hierzu gibt es ein paar Befehle:
- \fontencoding{}
- \fontfamily{}
- \fontseries{}
- \fontshape{}
- \fontsize{}{}
- \selectfont
fontencoding
Hiermit kann der entsprechende Zeichensatz gewählt werden.
\fontencoding{U}
Das U steht hier für UTF-8, welche Angaben möglich sind muss der Dokumentation des installierten Schriftpaketes entnommen werden.
fontfamily
Hiermit wird die Familie ausgewählt.
\fontfamily{cmr}
Angenommen ich möchte die Computer Modern Roman Schrift verwenden, so lese ich deren Dokumentation in dieser beschrieben ist das für deren Auswahl CMR als Fontfamilie anzugeben ist.
fontseries
Bei diesem Befehl wir die fontseries angegeben, ich möchte gerne bold extendet verwenden und schau in die Doku wo mir gesagt wird das hierzu bx anzugeben ist.
\fontseries{bx}
fontshape
Zu guterletzt wünsche ich mir als Schriftlage eine Kursive und schaue wieder in der Doku nach was hierfür falls vorhanden angegeben werden muss.
\fontshape{it}
fontsize
Die Schriftgrösse und der Zeilenabstand kann ebenfalls mit angegeben werden, als Beispiel wähle ich hier eine Grösse von 24,88 pt und einen Zeilenabstand bzw. Durchschuss von 5 pt.
\fontsize{24.88}{5}
selectfont
Selectfont ist ein Operator zum festlegen von Fonts und Schriftgrössen.
\selectfont
Beispiel - Computer Modern Roman
Ich möchgte hier noch schnell ein fertiges Beispiel Zeigen. Da die Computer Modern als Standart Schriftfamilie unter LaTeX verwendet wird ist mein Beispiel auf diese Schrift bezogen da sie jeder in seinem LaTeX System hat und so die verschiedenen Paramter probieren und testen kann, ohne zuerst irgend welche weiteren Schrifften runterladen und installieren zu müssen.
\begin{document}
\fontfamily{cmr} \fontseries{bx} \fontshape{it} \fontsize{14.4}{3} \selectfont
Computer Modern Roman bold extended italic
\end{document}
Schrift Paket
Es gibt derzeit ein Bündel von div. Schriften welches sich psnfss nennt und absolut zu empfehlen ist. Verfügbar ist es auf den CTAN Servern zum downloaden und anschliessenden installieren. Dieses Bündel ist AFAIK bei einer eueren LaTeX Version bereits dabei und beinhaltet mehrere diverse Schriften die ich im Anschluss kurz vorstellen möchte.
Tipp: Debian
Stand: 07/2007
Unter Debian befindet sich dieses Paket in texlive-latex-base und kann bequem via APT installiert werden.
Bevor wird die Schriften verwenden, sollte ein entsprechender Eintrag in die Präambel des Dokumentes geschrieben werden.
\usepackage[T1]{fontenc}
\usepackage{textcomp}
Durch die Angabe von T1 fontenc stellt die Font-Kodierung auf ein neueres Format um, das besser mit Umlauten funktioniert.
Das Paket textcomp lädt in LaTeX die TC-Schrifften für viele weiter Zeichen wie das Copyright oder Copyleft wie auch das Euro Symbol. Zudem alle Sonderzeichen aus ISO 8859-1.
Helvetica
Helvetice ist der Name einer Schriftart welcher weltweit geschützt ist und der Firma Linotype gehört. Sie ist eine Serifenlose Linearantiquare Schrift mit klassizistischem Charakter welche 1957 vom Grafiker Max Miedinger und Eduard Hoffmann entwikelt wurde. Ihr erster ursprünglicher Name war "Neue Haas-Grotesk" da Eduard Hoffmann der Geschäftsführer von der Haas'schen Schriftgiesserei AG war. Nach einer Übernahme von der D. Stempel AG bekamm die Schrift 1961 ihren Namen Helvetica unter dem sie Welt bekannt wurde. Im Jahre 1985 ist es zu einer weiteren Übernahme von Linotype gekommen.
Ein freier OpenSource Ersatz für Helvetica ist die "Nimbus Sans L Regular" Schrift welche von URW Software & Type kostenlos zu Verfügung gestellt wird.
\fontfamily{phv} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{m} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{phv} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{b} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{b} \fontshape{sc} \selectfont
\fontfamily{phv} \fontseries{mc} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{mc} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{mc} \fontshape{sc} \selectfont
\fontfamily{phv} \fontseries{bc} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{bc} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{bc} \fontshape{sc} \selectfont
Avant Garde
Die Avent Garde sollte zuerst überhaupt keine Schrift werden, sie ist der Name oder das Loge eines US-Kulturmagazines namens Avant Garde. Der Herrausgeber Ralph Ginzburg und Herb Lubalin suchten zu dem Namen dieses Magazienes eine einzigartige Schrift welche nach viel eigenem Testen und probieren am Ende Herbert F. Lubalin (1918 ? 1981) entworfen hatte. Die Avant Garde Schrift ist nicht für große Texte, d.h. den Mengen Satz geeignet. Am meisten wurde sie bisher in Werbung eingesetzt. Der bekanntetste Konzern welcher sie in einer Werbung 1975 verwendete war die Marke Addidas, zudem ist sie auf div. CD Covern zufinden. Im grossen und ganzen ist sie am besten für Titel oder Überschrifften geeignet. Auf Visitenkarten oder Briefköpfen würde sie sich bestimmt auch ganz gut machen.
\fontfamily{pag} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pag} \fontseries{m} \fontshape{sl} \selectfont
\fontfamily{pag} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pag} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pag} \fontseries{b} \fontshape{sl} \selectfont
\fontfamily{pag} \fontseries{b} \fontshape{sc} \selectfont
Bookman
Die Bookman Schrift wurde von Alexander Phemister im Jahr 1860 entwikelt. Es ist eine Serifen Schrift die eigentlich für die Verwendung in Büchern gedacht ist. Die sehr Populäre ITC Bookman stammt von ihr ab und wurde 1975 von Ed Benguiat designed .
\fontfamily{pbk} \fontseries{l} \fontshape{n} \selectfont
\fontfamily{pbk} \fontseries{l} \fontshape{it} \selectfont
\fontfamily{pbk} \fontseries{l} \fontshape{sc} \selectfont
\fontfamily{pbk} \fontseries{db} \fontshape{n} \selectfont
\fontfamily{pbk} \fontseries{db} \fontshape{it} \selectfont
\fontfamily{pbk} \fontseries{db} \fontshape{sc} \selectfont
Charter
Die Charter Schrift wurde von einem der bekanntesten Schriftsteller "Matthew Carter" im Jahr 1987 ins Leben gerufen. Er ist der Sohn des ebenfalls berühmnten Typografen Harry Carter. Matthew Carter zählt zu den bekanntesten der Computer Schriften Macher neben Hermann Zapf, Adrian Frutiger oder Erik Spiekermann. Desweiteren stammem weitere Schriften wie die Helvetica Compressed oder Shelly sowie Snell und Verdana von ihm.
\fontfamily{bch} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{bch} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{bch} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{bch} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{bch} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{bch} \fontseries{b} \fontshape{sc} \selectfont
Courier
Bei Courier handelt es sich um eine von Howard Kettler im Jahre 1956 entwikelte Schrift für Schreibmaschienen und Computer. Es ist wie bei Schreibmaschienen üblich, eine nicht proportionale Schrift mit sehr sarken Serifen. Verwendet werden die nicht proportionalen Schriften meist bei eMails, Programiersprachen und Computerterminales da sie über eine feste Zeichenbreite verfügen.
\fontfamily{pcr} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pcr} \fontseries{m} \fontshape{sl} \selectfont
\fontfamily{pcr} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pcr} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pcr} \fontseries{b} \fontshape{sl} \selectfont
\fontfamily{pcr} \fontseries{b} \fontshape{sc} \selectfont
New Century Schoolbook
Century Schoolbook wurde 1919 von Morris Fuller Benton entworfen welcher ein in den USA bekannter Typograf und Ingenieur war (1872–1948). Weitere von ihm recht bekannte Schriften sind Bodoni-Antiqua, Broadway, Century, Franklin Gothic, Clearface, Celtenham, und Stymie. Century Schoolnook ist ein etwas älterer Stiel mit Serifen welche für Schulbücher gedacht war und bei diesen auch verwendet wurde.
\fontfamily{pnc} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pnc} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{pnc} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pnc} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pnc} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{pnc} \fontseries{b} \fontshape{sc} \selectfont
Palatino
Die Palatino Schrift ist eine Französische Renaissance-Antiqua welche von Hermann Zapf im Jahre 1948 erfunden wurde. Diese Schrift wurde in der Nachkriegszeit Old-Style aus Deutschland geschaffen um auch auf minderwertigem Papier ein gutes Bild zu machen.
\fontfamily{ppl} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{ppl} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{ppl} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{ppl} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{ppl} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{ppl} \fontseries{b} \fontshape{sc} \selectfont
\fontfamily{pplx} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pplx} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{pplx} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pplx} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pplx} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{pplj} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pplj} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{pplj} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pplj} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pplj} \fontseries{b} \fontshape{it} \selectfont
In diesen Beispielen sehen ein paar Schriften doch fast gleich aus, man könnte meinen sie wären doppelt gelistet was natürlich nicht stimmt. Wir haben hier zum Teil drei unterschiedliche Schrift Familien welche nur sehr kleine aber feine Unterschiede aufweissen.
- ppl
- pplx
- pplj
Bei sehr genauem Hinsehen erkennen wir die kleinen Unterschiede.
\fontfamily{pplj} \fontseries{m} \fontshape{n} \selectfont
Palatino Medium Normal
\fontfamily{pplx} \fontseries{m} \fontshape{n} \selectfont
Palatino Medium Normal
\fontfamily{ppl} \fontseries{m} \fontshape{n} \selectfont
Palatino Medium Normal
Times
Die Times ist eine von Stanley Morison und Victor Lardent im Jahre 1931 entwikelte Barock-Antiqua-Schrift. Von der ursprünglichen Times existieren im heutigen Computerzeitalter viele verschiedene Versionen wie beispielsweise die Times New Roman welche nicht gleich Times ist ! Dem Computerzeitalter hat es die Times zu verdanken das sie so populär geworden ist, Fimren wie Apple Adobe oder Microsoft haben zum grossen Teil dazu beigetragen. Was die genaue Entstehung der Times Schrift angeht, so gibt es hier anscheinend verschidene Versionen. Man ist sich aber dennoch einig, das die Times für die Londoner Zeitung "The Times" entworfen wurde. Die Times New Roman wurde auf Wunsch von Microsoft eingeführt und von Monotypes entwickelt welche von der Times New Roman TS abstammt. Sie wurde damals extra an die deutschen Texte angepasst, da wir hier sehr viele Großbuchstaben in unserer Rechtscheibung verwenden im Vergleich zum Englischen.
Seit dem Jahre 2004 ist es in den USA Gesetzt alle Diplomatischen Arbeiten in der Times New Roman mit 14pt zu schreiben, anstelle der verherigen Courier New in 12pt.
Unter den Unix Systemen findet sich hier die "Nimbus Roman No9 L" von URW welche als Public Domain PostScripc Version der Times Roman freigegeben wurde. MacOS kommt mit der von Linotypes "Times Roman" und Microsoft mit der an Monotypes in Auftrag gegebener "Times New Roman".
Unter LaTeX schreiben wir in den hier vollgenden zur Times gezeigten Beispielen mit der richtigen originalen Times und nicht mit der Times New Roman.
\fontfamily{ptm} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{ptm} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{ptm} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{ptm} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{ptm} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{ptm} \fontseries{b} \fontshape{sc} \selectfont
Zapf Chancery
ermann Zapf der damalige Direktor der Stempel AG liebte die Kalligraphie, die Kunst des schön Schreibens. 1977 ging er als Professor an die Rochester Fachhochschule für Technologie in New York und entwar dort die Schriftkegel für Palatino, Optima, Zapf ( Chancery - im Jahre 1979 ) und Zapf Dingbats. Die Chancery ist Schulschrift, Englische Schreibschrift, Künstlerschreibschrift sowie für den Mengentext in machen Kinder Büchern geeignet.
\fontfamily{pzc} \fontseries{mb} \fontshape{it} \selectfont
Utopia
Die Utopia Schrift stammt aus dem Jahre 1989 und wurde designet von Robert Slimbach. Das großste und wohl bekannteste Beispiel zu dieser Schrift ist die Berliner Zeitung welche sie als Ausschrift nutzt. Ein kleiner Bericht vom 20.05.2005 über die Utopia in der Berliner Zeitung - online.
\fontfamily{put} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{put} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{put} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{put} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{put} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{put} \fontseries{b} \fontshape{sc} \selectfont
Eigene Schriften
Wer sich selbst einmal Schriften zugelegt hat für die er bezahlen musste, kann selbst diese unter LaTeX verwenden. Was allerdings dazu gesagt werden muss, das es nicht ganz einfach ist. Eventuell jeh nach dem in welchem Format diese Forliegen, müssen diese umgewandelt werden. So kann zum Beispiel eine Schrift im OpenType Format mit Hilfe von cfftot1 ins *.pfb Format converteirt bzw. umgewandelt werden.
Ich habe die ganze Geschichte ein einziges mal mit meiner Liblingsschrift der Sabon von Jan Tschichold gemacht, welche ich ebenfalls im OpenType Format vorliegen hatte. Das Umwandeln habe ich mit einem kleinen ShellScript bewerkstelligt.
#!/bin/sh mkdir -p pfb echo "Creating PostScript fonts ..." for font in otf/*.otf do base=$(basename "$font" .otf) cfftot1 "$font" "pfb/$base.pfb" done
Autor mit weiteren Infos zur Umsetzung sind hier zu finden.
The LaTeX Font Catalogue.
Font Guid PDF. ![]()
Für TrueType Font unter LaTeX (1/2)
Für TrueType Font unter LaTeX (2/2)
Hier das fertige Ergebnis in Sabon Italic, Sabon Medium und Sabon Kapitälchen.
Beste Schrift
Welche ist die beste Schrift überhaupt ?
Die beste Schrift überhaupt gibt es nicht, da es immer auf das ankommt was man letstenendes damit machen möchte. Die wohl belibtetste Schrift überhaupt wird Helvetica sein. Die Schrift Futura war zum Beispiele eine der populärsten überhaupt im 20. Jahrhundert. Welche Schrift aber die schönste ist, muss jeder für sich selbst entscheiden. Ich selbst verwende als Grundschrifftart bei all meinen Dokumenten die Standart LaTeX Schriffamilie Computer Modern, da diese nicht linear skaliert werden muss weil sie in vielen Grössen zu verfügung steht. Desweiteren wurde sie vom macher des TeX Systemes Donald E. Knuth entwikelt. Ich nehme daher einfach mal an, das eine von Knuth entwikelte Schrift mit Sicherheit nicht die schlechteste ist. Zudem gefällt mir noch die Schrift Sabon, welche vom Grossen Meister der neuen Typografie Jan Tschichold stammt.
Arial ist eine Schrift die von Robin Nicholas und Patricia Saunders entwikelt wurde. Da diese seit Windows 3.1 von MS mitgeliefert wird, ist es eine der am weitesten verbreiteten Schriften überhaupt. Arial ist eine Art leicht abgewandelte Helvetica mit nur recht kleinen Unterschiden, daher stehen Typografen dieser Schrieft doch recht skeptisch gegenüber. Bei Times New Roman ist es so ähnlich, sie wurde von Stanley Morison und Victor Lardent entworfen und hat ebenfalls ihre Bekanntheit der Firma Microsoft wie auch Apple und Adobe zu verdanken. Anscheinen konnte oder wollte Microsoft keine teuren Profi Schriften bei Windows oder ihrem MS-Office Paket mitliefern, was somit auch der Grund ist weshalb sich diese so hartnäckig halten. Zudem ist es vl. erwähnenswert zu sagen das die Times New Roman extra für den deutschen Raum angepasst wurde, da wir in unserer deutschen Rechtschreibung doch recht viele Grossbuchstaben im vergleich zu anderen wie Englischen verwenden. Die Times New Roman eignet sich daher nicht für jede Sprache.
Ohne andere Schriften schlecht reden zu wollen, muss gesagt werden das die LaTeX Standart Schrift wirklich eine gute Wahl ist. Es wurde hier einen großen Wert auf die Ästethik und die Funktionalität gelegt. Sie kann sich daher problemlos mit den Windows Pendanten oder sehr teuren Profi Schriftfamilien Messen lassen. Zudem ist es bei den Windows meist TrueType-Fonts so, das dessen Buchstaben bei den einzelnen Schriftgraden vergrössert oder verkleinert werden. Hierdurch erkennen sogar nicht Profies deutliche Defizite was bei der LaTeX Standartschriftfamilie nicht ist.
Welche Schriftklassifikation
Wir sollten in unserer heutigen Zeit als Schrift eine Antiqua Schrift verwenden. Denn die Antiqua Schrift ist eine Schrift unserer Zeit in der wir uns befinden. Wir sollten keine Fraktur mehr in unseren Texten verwenden und somit versuchen die für die damalig sehr gute Typografie nach zu äffen. Die Frakturen waren zu ihrer Zeit genau richtig, gehören allerdings nicht mehr in unsere Zeit. Wenn wir heutige Texte besser darstellen und gestallten wollen wie die damaligen, so können wir dies also nicht mit der Fraktur von damals schaffen, sondern müssen neue Dinge welche der heutigen Zeit entsprechen verwenden und mit hilfe dieser versuchen besser zu sein als die damaligen. Schwabacher ist eine sehr gute, wunderschöne Schrift, aber in der heutigen Zeit absolut fehl am Platz. In den damaligen Texten war sie genau passend, aber dies eben nur zur damaligen Zeit. Wir benötigen eine natürliche, einfache, gut leserliche und leichte Schrift, aber anscheinend ist dies noch nicht bis zu jedem durchgedrungen. Oder aus welchem Grunde wird zum Beispiel an Bahnhöfen der Stationsnahme noch so oft in Fraktur anstelle in Lateinischer Schrift geschrieben ? So fällt es anderen Ländern bzw. Völkern die bei uns zu Besuch oder auf der Durchreise sind noch schwerer diese Wörter zu entzifern.
Toller Fortschritt den wir da haben !
Mehr Mathematisches
Plotten von Funktionen mit PSTricks
Ein paar wichtige Dinge
Der erste Fehler
Den ersten Fehler macht man, wenn man seinen Quellcode pstricks.tex nennt. Das ist nämlich schon der Name des PSTricks-Paketes. Und deshalb erntet man Fehlermeldungen.
PSTricks auf dem Bildschirm betrachten - PDF erstellen
Leider kann der DVI-Betrachter viele Dinge nicht richtig darstellen! Wenn man seine Plotts richtig dargestellt haben möchte, dann muß man mindestens eine Postsciptdatei erstellen. Wenn man ein PDF haben möchte, dann kann man die Postscriptdatei mit ps2pdf in ein PDF umwandeln. Es funktioniert nicht, wenn man die DVI-Datei in ein PDF umwandeln will.
Allgemeine Parameter
Notwendige Pakete
Es ist völlig ausreichend, das Paket pst-3dplot zu laden. Falls man nur 2-D-Plotts zu Papier bringen will, dann reicht auch das Paket pst-plot. Für alle Beispiele hier in diesem Artikel reicht es, diese Zeile in die Präambel zu schreiben:
\usepackage{pst-3dplot}
Die Umgebung
PSTricks stellt eine Umgebung bereit, in die man plotten kann. Diese Umgebung reserviert Platz für den Plott auf dem Papier. Hier die Umgebung:
\begin{pspicture}[Grundlinie](x0,y0)(x1,y1)
Plott
\end{pspicture}
- (x0,y0) gibt die linke untere Ecke an, (x1,y1) gibt die rechte obere Ecke an.
- Der Parameter "Grundlinie" ist eine Zahl zwischen 0 und 1. Dieser Parameter steht per default auf 0. Falls man neben seinem Bild noch etwas schreiben möchte, empfiehlt es sich, diesen Parameter auf 0.5 zu setzen. Das sieht schön aus, ist aber Geschmacksache.
Um seinen Plott einzurahmen, gibt es den Befehl
\psframe[Parameterliste](x0,y0)(x1,y1)
Mit den optionalen Parametern kann man etwa die Linienstärke bestimmen. Die Defaulteinstellungen sind allerdings OK. Man kann die Parameter also einfach weglassen. Für (x0,y0)(x1,y1) setzt man am besten die gleichen Werte ein, wie für das pspicture.
Manchmal kann es passieren, das man über das Bild hinausplottet. Dann möchte man abschneiden, was über den Rahmen hinausragt. Dafür gibt es 2 Möglichkeiten:
1. Clipping:
\psclip{Irgendein Rahmen}
\endpsclip
Als Rahmen setzt man dann seinen psframe ein.
2. Die Sternchenversion von pspicture.
\begin{pspicture}*[Grundlinie](x0,y0)(x1,y1)
Plott
\end{pspicture}
Beide Versionen schneiden ab, was vielleicht über den Rand des Bildes ragt. Clipping funktioniert auch mit anderen Objekten. Auch innerhalb des Bildes. Damit ist unsere Umgebung fertig. Hier ist sie:
Die vollständige Umgebung
\begin{pspicture}[Grundlinie](x0,y0)(x1,y1)
\psclip{\psframe[Parameterliste](x0,y0)(x1,y1)}
Hier
wird
geplottet.
\endpsclip
\end{pspicture}
Diese vollständige Umgebung habe ich gleich im ersten Beispiel f(x)=x² benutzt. In den weiteren Beispielen habe ich auf den Rahmen und auf Clipping verzichtet.
Skalieren der Plotts
Es gibt mehrere Möglichkeiten, einen Plott zu vergrößern:
- Der Befehl \scalebox{Vergrößerung}{pspicture}. Das wird im Beispiel Sinusfunktion demonstriert.
- Man ändert die Längeneinheiten mit dem Befehl \psset{unit=1cm}. Unit=1cm ist die Defaulteinstellung. Ändert man diese auf unit=2cm, wird der Plott doppelt so groß. Interessant wird diese Möglichkeit, weil man mit dem Kommando \psset{xunit=1cm, yunit=1cm} die einzelnen Achsen unterschiedlich vergrößern oder verkleinern kann. Leider wirkt sich dieser Befehl nur auf die PSTricks-Objekte aus. Alle anderen Objekte, welche man in seinem pspicture plaziert, werden nicht vergrößert. Sie ändern nicht einmal ihre Lage im Bild. Mit dem Befehl \psset{unit=2cm} wurde das Beispiel "Sinusfunktion in der Ebene" vergrößert.
2-D-Plotts
Das Koordinatensystem
Um das Koordinatensystem darzustellen, gibt es den Befehl:
\psaxes[optionale Parameter]{->}(0,0)(x1,y1)(x2,y2)
- x1 gibt die linke Seite der x-Achse an
- x2 gibt die rechte Seite der x-Achse an
- y1 gibt die untere Seite der y-Achse an
- y2 gibt die obere Seite der y-Achse an.
Folgende Parameter sind vielleicht interessant:
- labels=all / x / y / none Die Defaulteinstellung ist all. Aber speziell in Verbindung mit dem \psgrid möchte man vielleicht keine Beschriftung haben. Dann setzt man labels=none.
- ticks=all / x / y / none Die Defaulteinstellung ist all.
- linewidth=dim In Verbindung mit dem \psgrid möchte man vielleicht dickere Achsen zeichen. Man könnte etwa linewidth=1pt wählen.
Die Parameter werden durch ein Komma, voneinander getrennt.
Das Gitternetz \psgrid
Das Gitternetz zeichnet man mit folgendem Befehl:
\psgrid[Parameter](0,0)(x1,y1)(x2,y2)
Mögliche Parameter:
- (x1,y1): sind die Koordinaten der linken unteren Ecke.
- (x2,y2): sind die Koordinaten der rechten oberen Ecke.
- gridwidth gibt die Dicke des Zeichenstiftes an. Ich habe sie im Beispiel etwas feiner auf 0.1pt gestellt.
- gridlabels gibt die Größe der Beschriftung an. Falls man keine Beschriftung wünscht, gibt man gridlabels=0pt an.
- subgriddiv=Anzahl Mit subgriddiv kann man das Gitternetz weiter unterteilen. Je größer die Anzahl, um so feiner ist die Unterteilung.
- griddots=Anzahl Wird dieser Parameter angegeben, dann wird das Gitter gepunktet. Falls man eine durchgezogene Linie wünscht, lässt man diesen Parameter weg.
- subgriddots Wenn man das Gitter mit subgriddiv weiter unterteilt, kann man mit subgriddots auch die Unterteilung gepunktet zeichnen.
Hier ein Beispiel:
\documentclass{article}
\usepackage{pst-plot}
\begin{document}
\begin{center}
\begin{pspicture}(-3,-1)(5,4)
\psgrid[gridwidth=0.1pt,gridlabels=9pt,subgriddiv=3,subgriddots=4](0,0)(-3,-1)(5,4)
\end{pspicture}
\end{center}
\end{document}
Die Plottfunktion
Die 2-D-Plottfunktion hat folgendes Aussehen:
\psplot[Parameter]{untere Grenze}{obere Grenze}{Funktion}
Interessante Parameter sind:
- plotstyle=line / curve / dots/... Der Defaultwert ist line. Diese Einstellung ist OK.
- plotpoints=Anzahl Die Anzahl ist hier auf 50 eingestellt. Das reicht auch meistens. Es wird aber in der Literatur ein Wert von 200 empfohlen.
- linecolor=red / green / cyan /.... Falls man mehrere Funktionen in einer Grafik plotten möchte, kann man sie unterschiedlich färben. Die Defaulteinstellung ist black.
- linestyle=solid / dotted / dashed Die Defaulteinstellung ist solid. Das ergibt eine durchgezogene Linie.
Die Angabe der Funktion ist etwas kompliziert. Man muß die Regeln der Umgekehrt Polnischen Notation UPN anwenden. Wenn man 2 Zahlen addieren möchte, rechnet man nicht a+b sondern a b add. Es werden also erst die Argumente angegeben, dann die Rechenoperation. Hier ein paar der wichtigsten:
- Addition: a b add liefert a+b
- Subtraktion: a b sub liefert a-b
- Multiplikation: a b mul liefert a*b
- Division: a b div liefert a/b
- Quadratwurzel: a sqrt liefert die Quadratwurzel von a
- Sinus: a sin liefert den Sinus von a. Das Argument wird in Grad (0-360) angegeben.
- Natürlicher Logarithmus: a ln liefert den natürlichen Logarithmus
- Potenz: a b exp liefert a^b
Es gibt noch mehr. Eine wichtige Operation ist noch folgende:
- Duplizieren: a dup liefert a a. a^2 berechnet man also so: a dup mul, das ist das gleiche wie a a mul.
Beispiele
Die Funktion f(x)= x^2
Das erste klassische Beispiel ist die Funktion f(x)=x^2.
\documentclass{article}
\usepackage{pst-plot}
\begin{document}
\begin{center}
\begin{pspicture}[](-5,-1)(5,9)
\psclip{\psframe(-5,-1)(5,9) }
% \psgrid[subgriddiv=1, gridlabels=0pt, griddots=5]
\psaxes[]{->}(0,0)(-4,0)(4,9)
\psplot[linecolor=red]{-3}{3}{x x mul}
\endpsclip
\end{pspicture}
\end{center}
\end{document}
Die Sinusfunktion
Das Argument der von PSTricks bereitgestellten Sinusfunktion muß in Grad angegeben werden. Das heißt:
- sin(90) = 1
- sin(180) = 0
- sin(270) = -1
- sin(360) = 0
Das lässt sich jedoch schlecht plotten. Wir machen es uns einfach, und plotten statt sin(x) einfach sin(180*x).
\documentclass{article}
\usepackage{pst-plot}
\usepackage[left=1cm, right=1cm]{geometry}
\begin{document}
\begin{center}
\scalebox{3}{
\begin{pspicture}(-0,-1)(4,1)
\psgrid[gridwidth=0.1pt, gridlabels=0pt,subgriddiv=1]
\psaxes[linewidth=0.5pt,labels=none, ticks=none]{->}(0,0)(-0,-1)(4,1)
\psplot[plotstyle=curve]{-0}{4}{x 180 mul sin}
\rput(2.2, -0.41){$2\pi$}
\rput(4.2, -0.41){$4\pi$}
\end{pspicture}
} % Hier endet die scalebox
\end{center}
\end{document}
3-D-Plotts
Die 3-D-Plottfunktion
Die 3-D-Plottfunktion hat folgende Gestalt:
\psplotThreeD[ Alpha=45, Beta=30,
hiddenLine=false,%
plotstyle=curve,%
drawStyle=xLines,%
yPlotpoints=80, xPlotpoints=80,%
linewidth=0.1pt]%
(xunten,xoben)(yunten,yoben){Die Funktion}
Beschreibung der Parameter:
- Alpha: Eine Erhöhung von Alpha dreht das Bild horizontal gegen den Uhrzeigersinn. Die Defaulteinstellung ist 45.
- Beta: Eine Erhöhung von Beta kippt das Bild nach vorn. Die Defaulteinstellung ist 30.
- hiddenLine: Mögliche Parameter sind true/false. Die Wirkung ist schwer beschreiblich. Einfach ausprobieren! Die Defaulteinstellung ist false.
- plotstyle: Mögliche Parameter: none / curve / line / dots /... Die besten Ergebnisse erhält man mit dem Parameter curve. Auch dots ist interessant. Hinweis: Die Defaulteinstellung ist none! Es wird also per Default keine Kurve gezeichnet.
- drawStyle: Mögliche Parameter sind xLines / yLines / xyLines. Also Kurven über die x-, y- oder beide Achsen. Die Defaulteinstellung ist xLines.
- yPlotpoints: Defaulteinstellung ist 25. Das ist wohl zuwenig.
- xPlotpoints: Defaulteinstellung ist 25.
- linewidth: Die Defaulteinstellung ist etwas zu dick! Ich habe sie hier etwas dünner (0.1pt) eingestellt. Das ist aber Geschmacksache.
Hinweis: Die Parameter Alpha und Beta muß man nicht in der Plottfunktion angeben. Man könnte sie auch im Befehl \psset angeben:
\psset{Alpha=45, Beta=30}
Dies hätte den Vorteil, das die Parameter auch für ein eventuell angegebenes Koordinatensystem gelten. Im folgenden Beispiel habe ich das so gemacht.
Beispiele
Die Sinusfunktion in der Ebene
Wir zeichnen mitten in eine Ebene den Ursprung. Und von dort breiten sich Sinusschwingungen in alle Richtungen aus. Die Funktion lautet:
f(x,y) = sin(sqrt(x^2+y^2)
\documentclass{article}
\usepackage{pst-3dplot}
\begin{document}
\begin{center}
\begin{pspicture}(-3,3)(3,8)
\psset{Alpha=65,Beta=70,unit=2.0cm}
\psplotThreeD[ plotstyle=curve,%
drawStyle=xLines,%
yPlotpoints=80,xPlotpoints=80,%
linewidth=0.1pt]%
(-3,3)(-3,3){x 180 mul dup mul y 180 mul dup mul add sqrt sin}
\end{pspicture}
\end{center}
\end{document}
Zum Vergleich werden wir dieses Beispiel auch einmal mit Maxima plotten. Wir starten Maxima und geben folgenden Code ein:
plot3d(sin(sqrt(x^2+y^2)),[x,-10,10],[y,-10,10],[grid,70,70], [plot_format, openmath]);
Zeichen und Symbole
Hier gehts um Zeichen z.B. für Währungen und Symbole etc.
Sonderzeichen
Die Darstellung von diversen Sonderzeichen funktioniert unter LaTeX ein bisschen anders als in üblichen Programmen.
Beispiel:
\begin{document}
\} \{ \_ \# \$ \% \& $\backslash$
\end{document}
Anführungszeichen
Um diverse Anführungszeichen etc. darzustellen, verwenden wir folgende Befehle:
\begin{document}
\flq \frq \flqq \frqq \glq \grq \glqq \grqq
\end{document}
Würde später im Dokument so aussehen:
Symbole & Zeichen
Hier nur schnell die wohl am häufigsten gebrauchten Symbole.
Copyright
\begin{document}
\copyright
\end{document}
Registriert
\begin{document}
\textregistered
\end{document}
TradeMark
\begin{document}
\texttrademark
\end{document}
Paragraph
Ein Beispiel für den Paragraphen 218, kann natürlich auch ein anderer sein.
\begin{document}
\S 218.
\end{document}
Weitere Symbole
Es gibt noch eine Vielzahl von weiteren Symbolen die ich hier alle garnicht aufzählen kann. Mir war es allerdings wichtig diese hier zu nennen und ein Beispiel zu zeigen, da ich der Meinung bin sie gehören zu den wichtigsten überhaupt beim schreiben von Büchern und Texten.
Ich möchte hier sehr gerne auf ein Dokument von Scott Pakin verweisen wenn man sich eine Übersicht über die unter LaTeX möglichen Sonderzeichen und Symbole verschaffen möchte.
Als PDF - Portable Document Format:
Währungszeichen
Die wichtigsten Währungszeichen im Überblick.
Euro
Bevor wir das Euro Währungszeichen verwenden können, sollten wir in unserer Präambel eurosym laden.
\usepackage{eurosym}
Um ein Eurosymbol nun darstellen zu können verwenden wir:
\begin{document}
\euro{}
\end{document}
Euro Beträge
Wer einen Geldbetrag anstelle des reinen Euro Symboles darstellen möchte, setzt zwischen die geschweiften Klammern den entsprechenden Betrag wie im Beispiel zu sehen.
\begin{document}
\euro{ 9.99}
\end{document}
Dollar
Die Darstellung des Dollars.
\begin{document}
\textdollar{}
\end{document}
Dollar Beträge
Hier wird genauso wie beim Eurobetrag vorgegangen, d.h. der eigentliche Betrag wird in die geschweiften Klammern geschrieben.
\begin{document}
\textdollar{ 9.99}
\end{document}
Pfund Sterling
Hier ein Beispiel für das englische Währungszeichen.
\begin{document}
\textsterling{}
\end{document}
Pfund Sterling Beträge
Wie auch schon bei den anderen Währungsbeträgen wird auch hier wieder der entsprechende Betrag zwischen die beiden geschweiften Klammern geschrieben.
\begin{document}
\textsterling{ 9.99}
\end{document}
Mathematische Zeichen und Symbole
Notwendige Pakete
Es empfiehlt sich, die Pakete amsfonts und amssymb einzubinden, da sonst nicht alle Zeichen und Buchstaben dargestellt werden können. Also die Zeilen
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsmath}
in der Präambel einfügen.
Verschiedene Zeichensätze
Das griechische Alphabet
Das griechische Alphabet erzeugen wir in der von Kile vorgegebenen Reihenfolge. Das ist ganz einfach: Ein Klick auf α erzeugt das Kommando \alpha. Wir nehmen die $...$-Umgebung und klicken einfach alle Buchstaben an. Wir erhalten diesen Code:
\begin{document}
$ \alpha\beta\gamma\delta\epsilon\varepsilon\zeta\eta\theta\vartheta\iota\kappa\lambda\mu\nu\xi\pi
\varpi\rho\varrho\sigma\varsigma\tau\upsilon\phi\varphi\chi\psi\omega\Gamma\Delta\Theta\Lambda\Xi
\Pi\Sigma\Upsilon\Phi\Psi\Omega $
\end{document}
Buchstaben mit 2 Strichen
Die Mengen der natürlichen, ganzen, rationalen, reellen und komplexen Zahlen werden oft durch Buchstaben mit 2 Strichen dargestellt.
\begin{document}
$\mathbb{N \quad Z \quad Q \quad R \quad C}$
\end{document}
Mathematische Symbole
Es gibt sehr viele mathematische Symbole. Man kann sie hier nicht alle aufführen. Hier eine kleine Auswahl aus der Spalte "Relation Symbols" von Kile:
\begin{document}
$ \leq \quad \geq \quad \subseteq \quad \supseteq \quad \in \quad \bigcap \quad \bigcup $
\end{document}
Interessant ist die unterschiedliche Wirkung der mathematischen Umgebungen. Der folgende Code wurde einmal in der $...$-Umgebung gesetzt. Und ein zweites Mal in der displaymath-Umgebung:
\bigcup_{i=1}^\infty
Noch ein paar wichtige Symbole aus der Spalte "Miscellaneous Symbols" von Kile:
\begin{document}
$ \forall \quad \infty \quad \exists \quad \partial \quad \emptyset $
\end{document}
Negationen: Viele mathematische Symbole haben eine Negation. Diese erhält man, indem man ein \not vor den Symbolbefehl stellt. Beispiel:
\begin{document}
$ \not \forall \not \in\ \not \leq \not \exists \not \subseteq $
\end{document}
Mathematische Sonderzeichen
Ein paar bekannte Sonderzeichen des Mathemodus welche ab und an mal benötigt werden können.
Winkelgrad
Hier das Winkelgrad Symbol:
\begin{document}
$ 360^\circ $
\end{document}
Celsius
Zur Angabe von Temperaturen in Celsius:
\begin{document}
$ 100\,^{\circ}\mathrm{C} $
\end{document}
Kleiner <
Uns stehen zwei Befehle zu Verfügung:
- \le
- \leq
\begin{document}
$ \le oder \leq $
\end{document}
Grösser >
Auch hier stehen uns zwei Befehle zu Verfügung:
- \ge
- \geq
\begin{document}
$ \ge oder \geq $
\end{document}
Maximal
\begin{document}
$ 500 ml. \max $
\end{document}
Mindestens
\begin{document}
$ 500 ml. \min $
\end{document}
Pfeile Diagonal
Hier ein paar diagonale Pfleile:
\begin{document}
$ \nearrow \nwarrow \searrow \swarrow $
\end{document}
Pfeile Horizontal, Vertikal, Oben, Unten
\begin{document}
$ \downarrow \uparrow \leftarrow \rightarrow $
\end{document}
Welches LaTeX ?
Meist stellt sich am Anfang die Frage welches LaTeX man nutzen soll, ich empfehle hier eigentlich immer das zu nutzen welches auch vom Distributor mitgeliefert bzw. unterstützt wird. Das TeXLive Projekt ist derzeit wohl das größte und das welches am ehesten zu empfehlen ist. Es gibt auch noch andere wie beispielsweise teTeX, welches derzeit leider auf Eis liegt. Auf deren Homepage wird momentan auch auf das TeXLive verwiesen.
Installation
Ich kann nicht auf die Installation von LaTeX unter jeder Distribution eingehen, da ich selbst nur eine verwende. Vielleicht findet sich ja der ein oder andere User und stellt ein paar Zeilen mit in diesen Artikel um anderen die Installation zu erleichtern.
openSUSE
OpenSUSE bis einschließlich Version 10.2 verwendet ausschließlich teTeX als LaTeX Distribution. Da man derzeit mit teTeX noch völlig problemlos arbeiten kann (das Projekt liegt erst seit Mai 2006 auf Eis), wird aufgrund eventuell schwierig aufzulösender Paketabhängigkeiten momentan davon abgeraten, TeXLive zu installieren. Das auf den Suse DVDs mitgelieferte teTeX sollte weiterhin verwendet werden.
Bei Suse 10.3 wurde TeXLive der neue Standard.
Debian
( Stand 05/2007 )
Die Installation umfasst das TeXLive oder teTeX mit ein paar weiteren Paketen die man so bei der täglichen Arbeit mit LaTeX benötigt.
Dank APT ist die Installation unter Debian ein Kinderspiel:
Laut Meldung vom 04.07.07 auf Pro-Linux wird im kommenden Debian Lenny als LaTeX Standard TeXLive verwendet werden.
TeXLive
Zuerst aktualisieren mit :
apt-get update
Dann installieren:
Erst nach der Installation der genannten Pakete Kile installieren !
Sollte jemand erst Kile installieren wollen, so wird anstelle TeXLive durch die Abhänigkeiten teTeX installiert !
apt-get install tex-common texlive-base texlive-base-bin texlive-common texlive-doc-base texlive-doc-de texlive-lang-german texlive-latex-base texlive-pdfetex preview-latex-style texlive-latex-extra texlive-pictures texlive-fonts-recommended
Jetzt kann Kile installiert werden. ( Vorausgesetzt man möchte es verwenden, schließlich reicht jeder einfache Text Editor. )
apt-get install kile kile-i18n
Es ist recht sinnvoll, zudem gleich KDVI und KPDF mit zu installieren falls es noch nicht vorhanden sein sollte.
apt-get install kdvi kpdf
KOMA-Script
Wer zu den LaTeX Standarddokumentenklassen noch das Paket KOMA-Script benötigt, kann dies für TeXLive so nachinstallieren:
apt-get install texlive-latex-recommended
Dieses Paket enthält noch weiteres wie z.B.
- HA-prosper -- Patches and improvements for prosper.
- anysize -- A simple package to set up document margins.
- booktabs -- Publication quality tables in LaTeX
- caption -- Customising captions in floating environments.
- cite -- Supports compressed, sorted lists of numerical citations.
- citeref -- Add reference-page-list to bibliography-items.
- crop -- Support for cropmarks.
- ctable -- Easily typeset centered tables.
- ec -- Computer modern fonts in T1 and TS1 encodings.
- euler -- Use AMS Euler fonts for math.
- everysel -- Provides hooks into \selectfont.
- everyshi -- Take action at every \shipout.
- extsizes -- Extends article and report with extra sized fonts.
- fancyref -- A LaTeX package for fancy cross-referencing.
- fancyvrb -- Sophisticated verbatim text.
- float -- Improved interface for floating objects.
- floatflt -- Wrap text around floats.
- fp -- Fixed point arithmetic.
- index -- Extended index for LaTeX including multiple indexes.
- jknapltx -- Macro package for TeX (the most popular).
- koma-script -- A bundle of versatile classes and packages
- listings -- Typeset source code listings using LaTeX.
- mdwtools -- Miscellaneous tools by Mark Wooding.
- memoir -- Typeset fiction, non-fiction and mathematical books.
- ntgclass -- "European" versions of standard classes.
- oberdiek -- Packages written by Heiko Oberdiek
- ps4pdf -- Use Postscript commands inside a pdfLaTeX document.
- psfrag -- Replace strings in encapsulated PostScript figures.
- rcs -- Use RCS (revision control system) tags in LaTeX documents.
- rotating -- No caption.
- seminar -- Overhead slides.
- setspace -- Set space between lines.
- subfig -- Figures broken into subfigures
- thumbpdf -- Thumbnails for pdfTeX and dvips/ps2pdf.
- ucs -- The ucs package.
- xkeyval -- Extension of the keyval package.
- mathpazo -- Pazo Math fonts and LaTeX package to typeset Palatino.
- powerdot -- The powerdot package.
- microtype -- An interface to the micro-typographic extensions of pdfTeX
teTeX
Zuerst aktualisieren:
apt-get update
Dann installieren:
apt-get install tex-common tetex-bin tetex-base tetex-extra tk-brief
Für die Verwendung von Kile.
apt-get install kile kile-i18n
Und wer es nicht schon installiert hat sollte KDVI & KPDF gleich mit installieren.
apt-get install kdvi kpdf
KOMA-Script
Wer zu den LaTeX Standarddokumentenklassen noch das Paket KOMA-Script benötigt, kann dies für teTeX so nachinstallieren:
apt-get install tk-brief
Dieses Paket enthält i.d.r. noch weiteres wie z.B.
- KOMA
- g-brief
- dinbrief
- letter
- brief
Info zu Kile
Was unbedingt nach der Installation von Kile, sofern man es verwendet, durchgeführt werden sollte, ist die Systemüberprüfung, welche einem das Programm bietet und i.d.r unter Einstellungen zu finden sein sollte. Falls Kile etwas wichtiges fehlen sollte, wird dies von der Systemüberprüfung angezeigt und kann vom User einfach nachinstalliert werden.
LaTeX Distributionen
- TeX Live Hierbei handelt es sich um ein CD lauffähiges LaTeX System.
- VTeX/Free Kostenfreie Distribution für Linux wie auch OS2.
- teTeX Eine Distribution für Unix Systeme, deren Entwicklung gerade auf Eis liegt.