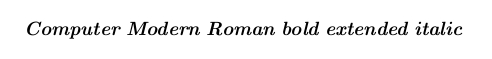LaTeX/Fortgeschrittene
| LaTeX: (1.) Einleitung - (2.) Schnellkurs - (3.) Teil 1 - Grundlagen - (4.) Teil 2 - Grundlagen - (5.) Fortgeschrittene - (6.) Literaturverzeichnisse - (7.) Zeichen und Symbole - (8.) LaTeX Distributionen - (9.) LaTeX Links |
Inhaltsverzeichnis
- 1 Fortgeschrittene
- 1.1 Für was ?
- 1.2 Seitenaufbau
- 1.3 Satzspiegel
- 1.3.1 Konstruktionsverfahren
- 1.3.2 Welches Konstruktionsverfahren
- 1.3.3 Satzspiegel der Standartklassen
- 1.3.4 Dimensionsparamter
- 1.3.4.1 Höhe Satzspiegel
- 1.3.4.2 Breite Satzspiegel
- 1.3.4.3 Kopfsteg
- 1.3.4.4 Linker Rand Einseitig
- 1.3.4.5 Linker Rand Zweiseitig
- 1.3.4.6 Seitenkopf zum Satzspiegel
- 1.3.4.7 Seitenkopfbereich
- 1.3.4.8 Seitenfuß zum Satzspiegel
- 1.3.4.9 Seitenfußbereich
- 1.3.4.10 Marginalie zum Satzspiegel
- 1.3.4.11 Marginalie Breite
- 1.3.4.12 Marginalie zur Randnotiz
- 1.3.4.13 Abstand zwischen Absatz
- 1.3.4.14 Zeilendurchschuss
- 1.3.4.15 Marginalien Seite
- 1.3.5 Layout Vergleich
- 1.3.6 Automatische Satzspiegelkonstruktion
- 1.4 Schriften
- 1.5 Mehr Mathematisches
Fortgeschrittene
In diesem Bereich Anwendungen für Fortgeschrittene soll es ein bisschen weiter gehen wie das was wir in den Grundlagen dieses Wiki Books Teil 1 und Teil 2 gelernt haben. Fortgeschrittene soll nicht heissen das es schwerer oder kompliziert wird und nur von Profis zu verstehen ist. In diesem Bereich sollen Dinge gezeigt und erklärt werden welche man nicht unbedingt bei der alltäglichen Arbeit benötigt oder dafür wissen muss. Würde dieser Teil so geschrieben werden das er nur von Profis verstanden würde, so wäre ich ein schlechter Autor und dies ein schlechtes Wiki.
Für was ?
Jeder der diesen Teil des Wiki Books liest, wird mit dem Textsatzprogramm LaTeX bereits gearbeitet haben.
Ich stelle nun einfach mal die Frage, für was genau verwendet ihr eigentlich LaTeX ?
Natürlich wird hier an erster Stelle die Antwort stehen:
- Um einen Text in Form von Artikeln, Berichte, Briefe oder sogar eines Buches schreiben zu können.
An zweiter Stelle kommt vermutlich:
- Um den zu verfassenden Text sauber, einheitlich und richtig darstellen zu können.
Ersteres ist natülich ganz klar: Wir benötigen kein Textsatzsystem, wenn wir nichts zu verfassen haben. Beim zweiten Punkt, der Darstellung
unseres Textes, den wir verfassen, kann LaTeX uns eine Menge an Arbeit abnehmen. Hierzu gehört zum Beispiel das Setzten von Überschriften an
die jeweils richtige Stelle. Das richtige Darstellen von beispielsweise Randnotizen oder auch Fußnoten. Genauso wird dafür gesorgt, dass wir
immer die entsprechend vorgegebenen oder bereits von Hand eingestellten Seitenränder, etc., einhalten, oder dass unser Satzspiegel an der richtigen
Stelle in unserem Dokument platziert wird.
Schön und gut, wenn uns so viel an Arbeit abgenommen wird, doch sollten wir nicht auch selbst wissen was mit einer "Nutzflache" im Dokument gemeint ist, wie sie aufgebaut ist, an welche Stelle sie steht und was darum herum existiert? Was ist ein Außensteg etc.?
Seitenaufbau
Was gibt es alles auf einer Seite bzw. kann es dort geben und wo wird es platziert. Diese Fragen soll hier schön verständlich beantwortet werden.
Zu einer Seite gehören oder können gehören:
- Satzspiegel
- Paginierung
- Kopfsteg
- Marginalien
- Toter Kolumnentitel
- Lebender Kolumnentitel
- Fußsteg
- Bundsteg
- Außensteg
Satzspiegel
Als Satzspiegel einer Seite, wird auch die sogenannte Nutzfläche in der Typografie bezeichnet. Wenn ich eine Seite mit einem niedergeschriebenem Text nehme, und diesen eigentlich Text mit einem Rahmen umrahme, sehe ich was ein Satzspiegel ist. Zum Satzspiegel gehören in der Regel keine Seitennummern ( Paginierungen ). Genausowenig gehört kein toter Kolumnentitel zum Satzspiegel. Marginalien ( Randnotzien ) gehören ebenso nicht zu einem Satzspiegel, zudem befindet sich ein Satzspiegel in einem Dokument stehts an ein und der selben Stelle. Das heisst, er kann nicht nach belieben auf jeder Seite hin und her geschoben werden. Desweitern wird ein Satzspiegel begrenzt durch die sogenanten Stege, welche den unbedruckten Bereich zwischen dem Satzspiegel und dem Rand darstellen. Die Spalten auch Kolumnen genannt mit dem eigentlichen Text oder auch Grafiken und Bildern gehören mit zum Satzspiegel. Gleiches gilt auch für die Fußnoten welche mit zum Satzspiegel gerechnet werden.
Paginierung
Mit Paginierung bezeichnet man das festlegen der Stelle an der die Seitennummer des Dokumentes sein soll. Eine Seite kann durchaus an mehreren Stellen die Seitennummer haben. Allerdings ist zu beachten, das die Stelle der Seitennummer an der diese angebracht ist durchgehen durch das gesamte Dokument fliesst. Dies soll heissen, das die Seitenzahl oder Seitenzahlen immer an der selben Stelle der einzelnen Seiten zu finden sein sollen.
Kopfsteg
Mit dem Wort Kopfsteg wird ebenfalls der "Obere Rand" bezeichnet. Dies ist der Bereich welche von der oberen wagerechten Kante des Blattes bis zum Satzspiegel reicht. Mit in den Kopfsteg kann zum Beispiekl auch der toter Kolumnentitel geschrieben werden. Hierbei sollte allerdings beachtet werden, das dieser nicht mit in den linken und rechten Außensteg gelangt, genauso wenig in den Bundsteg bei Büchern.
Marginalien
Marginalien sind wie Randnotzien kleine leichte Ergänzungen zum Text welche meistens im rechten Außensteg ( Rechter Rand ) zufinden sind. Die kleinen leichten Marginalien werden in der Regel nicht mit zum Satzspiegel dazu gerechnet. Es können auch nur Symbole oder andere kleine Elemente sein.
Viele oder sehr grosse Marginalien welche viel Platz benötigen werden mit zum Satzspiegel gerechnet.
Der Grund weshalb Marginalien meistens auf die Rechte Seite geschrieben werden liegt daran das wenn man das fertige Blatt ebheften würde durch den Rand welcher auf der linken Seite entsteht einen Bereich ( Bundsteeg z.B. bei einem Buch ) hat der sehr schlecht ins Auge fällt. Man könnte die Marginalien aber auch anstelle der rechten auf die Linke Seite schreiben wenn man dies wünscht.
Toter Kolumnentitel
Der sogenannte tote Kolumnentitel wird nicht mit zum Satzspiegel gezählt und ist bzw. sollte immer durch das gesamte Dokument an einer festen Stelle stehen. Desweiteren befindet sich der toter Kolumnentitel entweder im oberen oder unteres Rand bzw. im Bereich des Kopf- u. Fußsteges. Er sollte klein, leicht und dezent gehalten werden, so das er den eigentlichen Satzspiegel nicht stört.
Lebender Kolumnentitel
Der lebender Kolumnentitel ist Teil des Satzspiegels und wird in dessen erste Zeile geschrieben. Dieser lebender Kolumnentitel sollte vortlaufend im Dokument ebenfalls immer an der selben Stelle zu finden sein. Sollte auf einer Seite der lebender Kolumnentitel und oder eine Überschrift an der selben Stelle stehen, so fällt der lebender Kolumnentitel weg. Sollte bei der Paginierung eine Seitenzahl mit in den Bereich des Satzspiegels kommen, so gehört diese Seitenzahl mit in die selbe Zeile innerhalb des Satzspiegels wie auch der lebender Kolumnentitel.
Fußsteg
Mit Fußsteg wird ebenfalls der untere Rand bezeichnet. Dieser ist der Bereich von der waagerechten Seite des Blattes bis zum Satzspiegel auf der Seite. Mit in den Fußsteg kann zum Beispiekl auch der toter Kolumnentitel geschrieben werden. Hierbei sollte allerdings beachtet werden, das dieser nicht mit in den linken und rechten Außensteg gelangt, genauso wenig in den Bundsteg bei Büchern.
Bundsteg
Der Bundsteg ist der Bereicht welcher beim erstellen eines Buches für die Bindung benötigt wird. In einem Buch habe ich so auf der rechten Buchseite einen Bundsteg auf der linken Seite des Blattes, und auf der Linken seite der Buchseite einen Bundsteg auf der Rechten Seite des Blattes. Zudem ist der Bundsteg ein später nicht mehr sichtbarer Bereicht, da dieser für die Buchbindung verwendet wird.
Außensteg
Der Außensteg ist der Bereich, welcher auch als äußerer Rand bezeichnet wird. Es ist der Teil, welcher von der senkrechten Papierkante am linken wie auch am rechten Rand bis zum Satzspiegel reicht.
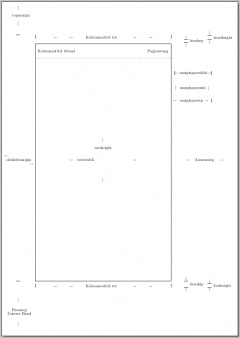
Darstellungsbeispiel
Hier wurden nun mehrere Dinge genannt und mit Hilfe von wörtern beschrieben. Da es für manche jedoch einfacher ist dies zu verstehen wenn sie es bildlich vor sich haben, so habe ich das ganze mal schnell in LaTeX geschrieben um es verständlicher zu machen. Der eigentliche Quelltext befindet sich im Anschluss unter dem Bild. Hierbei sollte allerdings erwähnt werden, das ich die Paginierung ( Seitennummerierung ) im Beispiel weg gelassen habe. Einzig die Paginierung im Satzspiegel befindet sich im Beispiel.
Quellcode der Darstellung:
\begin{document}
\fbox{
\begin{picture}(331,594)
\put(-6.0,610.0){\line(0,1){10.0}}
\put(337.0,610.0){\line(0,1){10.0}}
\put(122.0,610.0){Kolumnentitel tot}
\put(80.0,610.0){$ \leftarrow $}
\put(40.0,610.0){$ \leftarrow $}
\put(240.0,610.0){$ \rightarrow $}
\put(280.0,610.0){$ \rightarrow $}
\put(0.0,575.0){Kolumnentitel lebend}
\put(+278.0,575.0){Paginierung}
\put(-6.0,560.0){\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots\dots}
\put(140.0,300.0){Satzspiegel}
\put(80.0,300.0){$ \leftarrow $}
\put(240.0,300.0){$ \rightarrow $}
\put(162.0,350.0){$ \uparrow $}
\put(162.0,250.0){$ \downarrow $}
\put(-6.0,-20.0){\line(0,1){10.0}}
\put(337.0,-20.0){\line(0,1){10.0}}
\put(122.0,-20.0){Kolumnentitel tot}
\put(80.0,-20.0){$ \leftarrow $}
\put(40.0,-20.0){$ \leftarrow $}
\put(240.0,-20.0){$ \rightarrow $}
\put(280.0,-20.0){$ \rightarrow $}
\put(-72.0,300.0){Aussensteg}
\put(-69.0,290.0){Bundsteg}
\put(-84.0,300.0){$ \leftarrow $}
\put(-22.0,300.0){$ \rightarrow $}
\put(398.0,300.0){Aussensteg}
\put(375.0,300.0){$ \leftarrow $}
\put(459.0,300.0){$ \rightarrow $}
\put(-55.0,-3.0){\line(1,0){10.0}}
\put(-65.0,-80.0){Fusssteg}
\put(-77.0,-90.0){Unterer Rand}
\put(-52.0,-55.0){$ \uparrow $}
\put(-52.0,-115.0){$ \downarrow $}
\put(-55.0,597.0){\line(1,0){10.0}}
\put(-65.0,670.0){Kopfsteg}
\put(-75.0,660.0){Oberer Rand}
\put(-52.0,685.0){$ \uparrow $}
\put(-52.0,647.0){$ \downarrow $}
\put(367.0,450.0){Marginalien}
\put(353.0,450.0){$ \leftarrow $}
\put(422.0,450.0){$ \rightarrow $}
\put(440.0,448.0){\line(0,1){10.0}}
\put(345.0,448.0){\line(0,1){10.0}}
\end{picture}
}
\end{document}
Satzspiegel
Wir haben im oberen Teil erfahren was ein Satzspiegel ist und was er beinhalten kann. Nun geht es darum den Satzspiegel an die richtige Stelle auf einer Seite zu setzen und seine Prosition zu bestimmen.
Konstruktionsverfahren
Für die Bestimmung des Satzspiegel gibt es verschiedene Verfahren.
- Goldener Schnitt
- Rastersystemverfahren
Hinweis: Die hier gezeigten Beispiele sind geeignet für einen beidseitigen Druck wie beispielsweisse bei Büchern etc.
Für Briefe oder Manuskripte welche einseitig bedruckt werden, sind andere Werte und Prositionen für den Satzspiegel sinvoller.
Beim einseitigen Druck sollte das Seitenverhältniss etwa so sein:
- Kopfsteg und Fußsteg 1 : 2
- Linker Außensteg und rechter Außensteg 1 : 1
Das im Beispielbild gezeigte Verhältniss entspricht bereits dem Standart im europäischer Sprachraum. Bei den Voreinstellungen der LaTeX Standartklassen ist dies nicht so, da diese den Amerikanischen Layouts entsprechen.
Hinweis: Da es bei einem einseitigen Druck wie z.B. einem Aufsatz für die Schule keine Bindung wie bei einem Buch gibt, sollte man hier an die eventuelle Lochung denken und den linken Rand dementsprechend anpassen. Beim anpassen dieses Randes, vl. an die Grösse von "Lochverstärkerringen" denken falls solche eingesetzt werden sollten. Optisch recht schon anzusehen ist wenn rechts neben den Löchern genau so viel Platz wie links zum Blattrand gelassen wird. Bei den Schnellheftern wie sie auch gerne für Bewerbungen verwendet werden sollte unbedingt darauf geachtet werden das keinerlei Text unter der Klemmleiste verschwindet. Zudem möchte ich hier erwähnen das es sich bei einer Bewerbung meist um Einzeldokumente handelt welche aus unterschiedlichem Papier bestehen. Die erste Seite jedes Einzeldokumentes wirkt in der Regel für sich alleine.
Rastersystemverfahren
Ich möchte hier das Rastersystemverfahren zur Bestimmung des idealen Satzspiegels bei einer üblichen DIN A4 Seite zeigen.
Unter einem Rastersystem versteht man ein Ordnungssystem oder auch Gestaltungsraster. Hier durch soll die Vermittlung der einzelnen Informationen verbessert werden.
Satzspiegel erstellen
Beim erstellen des Rasters wird mit dem eigentlichen Satzspiegel begonnen. Dieser darf auf der eigentlichen Seite nicht zu weit oben liegen, da es sonst den Anschein macht der Text würde beim betrachten davon fliegen. Auf der anderen Seite muss man dafür sorgen das der Satzspiegel nicht zu weit unten liegt. Da dies beim Betrachten erdrückend wirkt. Bei den Rändern sollten ästhetisch Proportionen gewählt werden. Wichtig bei Büchern ist das hierbei der Bundsteg nicht auser acht gelassen wird. Da wir für das Binden eines Buches ebenfalls einen entsprechenden Bereich ( Bundsteg ) benötigen, sollte dieser mit eingerechnet werden. Bei einer linken Buchseite haben wir so den Bundsteg auf der rechten Papierseite und bei einer rechten Buchseite befindet sich der Bundsteg auf der linken Papierseite.
Spaltenbreite
Nachdem der Satzspiegel sowei fertiggestellt wurde wird dieser in einzelne Felder bzw. Spalten unterteilt. Wie viele Spalten benötigt werden liegt ganz alleine an der Struckturierung des Satzspiegels und dessen Menge des Inhaltes. Die Spaltenbreite kann also 1, 2, 3 oder 4, 5, 6 und mehr Spalten beinhalten. Je grösser zum Beispiel die Schrift ist welche verwendet wird, desto breite müssen die einzelnen Spalten sein.
Rasterfelder
Nachdem wir die Spalten welche Vertikal sind erzeugt haben, schreiten wir zu den Feldern welche durch horizontallinien hinzugefügt werden. Wie viele Felder man auf diese Art und Weise erstellen möchte liegt einzig und alleine beim Gestalter und sollte von diesem an den einzusetzenden Inhalt angepasst werden.
Schrift
Um die genaue Höhe des Satzspiegels bestimmen zu können, benötigen wir:
- Schriftart
- Schriftgrösse
- Zeilendurchschuss
Ein Zeilendurchschuss bezeichnet den Abstand der Unterlänge eines Kleinbuchstabens, bis zur Oberkante eines darunter angeordneten Großbuchstabens oder Kleinbuchstabens, je nach dem welches höher hinauf ragt.
Der Quellcode zum Beispiel des Zeilendurchschuss:
\begin{document}
\begin{picture}(300,300)
\put(-35.0,20.0){\line(1,0){300}}
\put(-35.0,12.0){\line(1,0){300}}
\put(-38.0,22.0){$ \downarrow $}
\put(-38.0,4.0){$ \uparrow $}
\begin{Huge}
\put(0.0,25.0){Ein Durchschuss Beispiel}
\put(0.0,-5.0){wird hier gezeigt}
\end{Huge}
\end{picture}
\end{document}
Wählen wir nun eine Schriftgrösse von 10pt mit einem Zeilendurchschuss von 3pt kann man zählen wie viele Zeilen in den Seitenspiegel hinein passen. Hier zu muss man allerdings die aller erste Zeile mit der Oberkante des Satzspiegels zueinander ausrichtet. Das heisst eine gemeinsame Bezugslinie finden. Dann werden alle Zeilen welche in unseren Satzspiegel passen abgezählt.
Nun beginnen wir mit dem Rechnen:
Angenommen in unseren Satzspiegel passen 50 Zeilen hinein, so müssen wir von dem Wert 50 einmal 2 abziehen für die Zeilen der Rasterfeldabstände.
( Zeilensumme abzüglich der Rasterfeldabstände ) 50 - 2 = 48
Dies wird nun durch die gewünschte Anzahl der Rasterfelder welche wir haben geteilt.
Bei beispielsweisse 3 Feldern, rechnen wir 48 durch 3
48 : 3 = 16
Ein weiteres Beispiel bei 6 Feldern könnte so aussehen:
50 - 2 = 48 : 6 = 8
Nun fehlen uns noch die Vertikalen Abstande unserer Felder. Dazu müssen wir nun die Unterkante eines unserer Rasterfelder an der Grundlinie der Unterkante ausrichten. Die Oberkante des Feldes wird an die Oberkannte eines Großbuchstabens der benutzten Schrift bündig gesetzt.
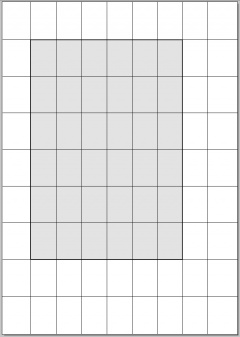
9er Rastersystemteilung
Hier ein Beispiel einer Satzspiegelkonstruktion einer neuner Rastersystemteilung. Dieses beispiel wurde von mir unter LaTeX erstellt und deren Quellcode steht direkt unter der Abbildung.
Diese Seite wurde horizontal u. vertikal in die gleiche Anzahl von Rasterfeldern aufgeteilt. Am inneren u. oberen Rand bleiben jeweils ein Rasterfeld frei, am äusseren und unteren jeweils zwei.
Hier der dazugehörige Quellcode:
\begin{document}
\begin{center}
\begin{picture}(583,841)
\put(65.0,-3.0){\line(0,1){845}}
\put(131.0,-3.0){\line(0,1){845}}
\put(195.0,-3.0){\line(0,1){845}}
\put(259.0,-3.0){\line(0,1){845}}
\put(323,-3.0){\line(0,1){845}}
\put(387,-3.0){\line(0,1){845}}
\put(451,-3.0){\line(0,1){845}}
\put(515,-3.0){\line(0,1){845}}
\put(-7.0,93.0){\line(1,0){598}}
\put(-6.0,187.0){\line(1,0){598}}
\put(-6.0,280.0){\line(1,0){598}}
\put(-6.0,373){\line(1,0){598}}
\put(-6.0,466.0){\line(1,0){598}}
\put(-6.0,559.0){\line(1,0){598}}
\put(-6.0,652.0){\line(1,0){598}}
\put(-6.0,745.0){\line(1,0){598}}
\put(65.0,186.0){\line(1,0){386}}
\put(65.0,744.0){\line(1,0){386}}
\put(64.0,186.0){\line(0,1){558}}
\put(450.0,186.0){\line(0,1){558}}
\end{picture}
\end{center}
\end{document}
Goldener Schnitt
Der Goldene Schnitt spielt beim Satzspiegel eine grosse Rolle, da dieser in seiner Art sehr harmonisch ist. Das wohl beste Beispiel für den Goldenen Schnitt ist die original Gutenberg Bibel. Gutenberg selbst, teilte bereits das Papier nach dem Goldenen Schnitt. Desweiteren findet man die Harmonische Einteilung vom Goldenen Schnitt in der freien Natur wie beispielsweise beim Schachtelhalm und Eichenblatt. Genauso in der Kunst und Architektur.
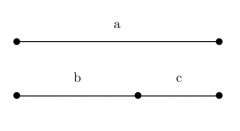
Hier ein einfaches Beispiel für einen Goldenen Schnitt:
Der Quellcode zur Zeichnung:
\begin{document}
\begin{picture}(300,300)
\put(-35.0,60.0){\line(1,0){150}}
\put(-35.0,60.0){\circle*{5.0}}
\put(115.0,60.0){\circle*{5.0}}
\put(37.0,70.0){a}
\put(-35.0,20.0){\line(1,0){150}}
\put(-35.0,20.0){\circle*{5.0}}
\put(115.0,20.0){\circle*{5.0}}
\put(55.0,20.0){\circle*{5.0}}
\put(7.0,30.0){b}
\put(83.0,30.0){c}
\end{picture}
\end{document}
- a = b + c
Die Länge (c) muss sich zur Länge (b) so verhalten wie die Länge (b) zur Länge (a).
Mathematisch gesehen bezeichnet der Goldene Schnitt also ein Teilungsverhältnis. Hierbei wird also eine Strecke namens (a) zuerst in zwei weitere Teile unterteilt. So das sich die größere Teilstrecke (b) proportional zur Gesamtstrecke verhält wie die kleinere Teilstrecke (c) zu der größeren Teilstrecke (b).
Wieso nun der Goldene Schnitt ?
Nun, das menschliche Auge sieht eine Fläche welche im Verhältnis 3:5 oder 2:3 ist sehr harmonisch. Genau genommen 1 : 1,618.
Bereits die Griechen hatten herraus gefunden das auch in den einzelnen Proportionen des menschlichen Körpers sich genau dieses Teilungsverhältnis wiederfindet. Dies ist auch ein weiterer Grund weshalb wir genau dieses Teilungsverhältnis so angenehm empfinden.
Der Goldene Schnitt besagt also das sich der Satzspiegel nicht genau in der mitte des Blattes befinden soll. Sondern mehr nach links oder rechts außen oder mehr ins obere des Blattes, da hierdurch mehr Spannung entsteht als wenn der Satzspiegel genau in der Mitte wäre.
Ich bin mir sicher das nun jeder weis was damit gemeint ist, man kennt es zum Beispiel auch von der Fotografie. Hierbei wird genauso bei der Bildgestaltung versucht ein Objekt nicht genau in die Mitte des Bildes zu setzen da wir so nicht wirklich Spannung in das Bild hineinbringen können.
Darstellungsbeispiel
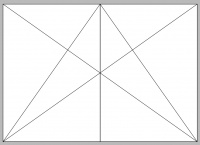
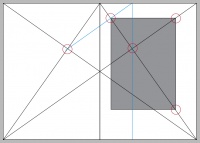
Satzspiegelkonstruktion einer Doppelseite nach dem Goldenen Schnitt:
- Abb. 1: Die Diagonalen werden über die Doppelseite konstruiert und die Einzelnseiten zeigen ebenfalls die Diagonalen von oben innen, nach unten aussen.
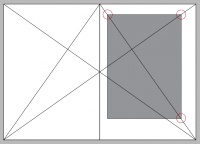
- Abb. 2: Die oberen Ecken des Rechtecks, die unteren äusseren Ecken liegen auf den konstruierten Diagonalen. Desto weiter oben u. außen die obere innere Ecke gewählt werden, desto größer wird der Satzspiegel und umso kleiner werden die Papierränder.
- Abb. 3: Satzspiegel im Verhältnis des Goldenen Schnittes.
Welches Konstruktionsverfahren
Wir haben nun gelernt was ein Satzspiegel ist und wozu dieser benötigt wird. Welches Verfahren man nun zur generierung des Satzspiegels verwendet bleibt jedem selbst überlassen. Vielen gefällt zum Beispiel bei einem Satzspiegel welcher mit dem Goldenen Schnitt erstellt wurde nicht das dieser bei einer Doppelseite so weit oben am Kopfsteg und am linken/rechten Außensteg liegt. Am Ende ist alles eine reine Geschmacksache die vom Gestalter dementsprechend gewählt wird.
Satzspiegel der Standartklassen
Wenn wir mit LaTeX unsere Dokumente erstellen, wundern wir uns doch des öffteren über die recht breiten Außenstege bzw. Seitenränder. Als erstes muss hier erwähnt werden, ( dies ist richtig und absolut korrekt ) so wie es ist. Wir selbst sind es einfach nur gewohnt Seitenlayouts anzusehen mit wesentlich geringeren Seitenrändern da dies bei uns hier in der Union ( europäischer Sprachraum ) so üblich ist. Die LaTeX Standartdokumentenklassen verwenden oder halten sich hier an die amerikanische Layouts.
Bei der Auswahl einer der entsprechenden Standartklassen unter LaTeX wird zudem auch der Satzspiegel und weiteres wie beispielsweisse die Außenstege / Seitenränder etc. festgelegt.
Hier zuerst eine Auswahl der Klassenoptionen des Seitenlayoutes, da sich bei der Wahl dieser auch zudem zahlreiche andere Dinge wie u.a. auch der Satzspiegel in seiner Aufteilung etc. verändert.
Bei uns übliche Grössen ( EU )
- a4paper = 210 × 297 mm ( Viertelbogen - Briefpapier, Formulare, Hefte, Zeitschriften, Kataloge )
- a5paper = 148 × 210 mm ( Blatt - Notizblöcke, Schulhefte )
- b5paper = 176 × 250 mm ( Bücher )
Bei uns nicht übliche Grössen ( US )
- letterpaper = 8 1/2 × 11 Zoll
- legalpaper = 8 1/2 × 14 Zoll
- executivepaper = 7 1/4 × 10 1/2 Zoll
Wer mit der Gestaltung bei Verwendung der Standartklassen so nicht zu frieden ist, kann hier auch selbst Hand anlegen. Mit Hilfe der Dimensionsparameter auf welche wir gleich näher eingehen werden können so zahlreiche Parameter verändert werden.
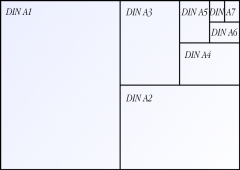
ISO Papier Formate
Eben wurden ein paar Papierformate aufgelistet, für ein besseres Verständniss habe hier ich eine kleine Grafik angefertigt um die entsprechenden Grössenunterschiede besser wahr zu nehmen.
Tabellarische Übersicht
| DIN-A | DIN-B | DIN-C | DIN-D | DIN-E | |
|---|---|---|---|---|---|
| 1 | 594 × 841 | 707 × 1000 | 648 × 917 | 545 × 771 | 560 × 800 |
| 2 | 420 × 594 | 500 × 707 | 458 × 648 | 385 × 545 | 400 × 560 |
| 3 | 297 × 420 | 353 × 500 | 324 × 458 | 272 × 385 | 280 × 400 |
| 4 | 210 × 297 | 250 × 353 | 229 × 324 | 192 × 272 | 200 × 280 |
| 5 | 148 × 210 | 176 × 250 | 162 × 229 | 136 × 192 | 140 × 200 |
| 6 | 105 × 148 | 125 × 176 | 114 × 162 | 96 × 136 | 100 × 140 |
| 7 | 74 × 105 | 88 × 125 | 81 × 114 | 68 × 96 | 70 × 100 |
| 8 | 52 × 74 | 62 × 88 | 57 × 81 | ||
| 9 | 37 × 52 | 44 × 62 | 40 × 57 | ||
| 10 | 26 × 37 | 31 × 44 | 28 × 40 |
Dimensionsparamter
Mit unseren Dimensionsparametern ist es möglich, sämtliche für die Darstellung benötigte Werte zu ändern. Dies können Seitenränder, Abstände von Kopf und Fuß etc. sein.
Höhe Satzspiegel
\setlength{\textheight}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hierdurch wird die Höhe des Satzspiegels bestimmt. Die Höhe ist zwischen Kopf und Fußbereich in denen zum Beispiel auch der tote Kolumnentitel steht. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Breite Satzspiegel
\setlength{\textwidth}{220mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hierdurch wird die Breite des Satzspiegels bestimmt. Dies ist der Bereich in welchem unser eigentlich Text steht. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Kopfsteg
\setlength{\topmargin}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Er setzt den Abstand zwischen unserem oberen Blattrand und dem Seitenkopf. Der Seitenkopf ist der Bereich in welchem auch unser tote Kolumnentitel stehen kann. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Linker Rand Einseitig
\setlength{\oddsidemargin}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Er setzt die Breite des Aussensteges, dies ist der Bereich vom linken Blattrand bis hin zum Satzspiegel. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Linker Rand Zweiseitig
\setlength{\evensidemargin}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Wird ein zweiseitiges Dokument erstellt, so wird hier der Wert des linken Randes vom rechten Blatt eingestellt. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenkopf zum Satzspiegel
\setlength{\headsep}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hier wird der Abstand zwischen dem Seitenkopf und dem Satzspiegel bestimmt. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenkopfbereich
\setlength{\headheight}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Mit diesem Befehl wird die Höhe angegeben des Bereiches welcher für den Seitenkopf reserviert wird. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenfuß zum Satzspiegel
\setlength{\footskip}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Legt den Abstand des Seitenfußes bis zum Satzspiegel fest. Im Seitenfuß kann zum Beispiel ein toter Kolumnentitel stehen. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Seitenfußbereich
\setlength{\footheight}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hier wird die Höhe des Bereiches bestimmt welcher für den Seitenfuß reserviert wird. Gleich wie beim Seitenkopfbereich. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Marginalie zum Satzspiegel
\setlength{\marginparsep}{20mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Mit diesem Befehl legen wir den Abstand zwischen unserem Satzspiegel und einer Marginalie fest. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Marginalie Breite
\setlength{\marginparwidth}{10mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Wir können hiermit die Breite des für eine Marginalie bestimmten Bereiches festlegen. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Marginalie zur Randnotiz
\setlength{\marginparpush}{30mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. Hier können wir den mindest Abstand angeben welcher vertikel zwischen mehreren Marginalie sein soll. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Abstand zwischen Absatz
\setlength{\parskip}{5mm}
Dieser Befehl ist für die Verwendung in die Präambel mit aufzunehmen. So wird der Abstand zwischen mehreren aufeinandervollgenden Absätzen angegeben. In diesem Beispiel wurde die Maßeinheit ( mm ) verwendet. Es können aber genauso gut auch ( pt ) für die Punkt Höhe verwendet werden.
Zeilendurchschuss
\setlength{\baselineskip}{12pt}
Der Zeilendurchschuss kann hiermit beeinflusst werden. Man verwendet i.d.R ca. 20% bis 30% der Schriftgrösse. D.h. bei einer 10pt grossen Schrift, sollte der Durchschuss ca. 12pt bis 13pt betragen.
Darstellungsbeispiele
Für ein besseres Verstehen habe ich das ganze mal grafisch versucht darzustellen. Der Quellcode ist wie immer unterhalb des Bildes zu finden.
Hier der dazugehörige Quellcode:
\begin{document}
\fbox{
\begin{picture}(331,594)
\put(-6.0,610.0){\line(0,1){10.0}}
\put(337.0,610.0){\line(0,1){10.0}}
\put(122.0,610.0){Kolumnentitel tot}
\put(80.0,610.0){$ \leftarrow $}
\put(40.0,610.0){$ \leftarrow $}
\put(240.0,610.0){$ \rightarrow $}
\put(280.0,610.0){$ \rightarrow $}
\put(0.0,575.0){Kolumnentitel lebend}
\put(+278.0,575.0){Paginierung}
\put(-6.0,560.0){\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots
\dots\dots\dots\dots\dots\dots\dots\dots}
\put(143.0,330.0){textheight}
\put(100.0,300.0){textwidth}
\put(80.0,300.0){$ \leftarrow $}
\put(162.0,350.0){$ \uparrow $}
\put(162.0,250.0){$ \downarrow $}
\put(240.0,300.0){$ \rightarrow $}
\put(-6.0,-20.0){\line(0,1){10.0}}
\put(337.0,-20.0){\line(0,1){10.0}}
\put(122.0,-20.0){Kolumnentitel tot}
\put(80.0,-20.0){$ \leftarrow $}
\put(40.0,-20.0){$ \leftarrow $}
\put(240.0,-20.0){$ \rightarrow $}
\put(280.0,-20.0){$ \rightarrow $}
\put(-80.0,300.0){oddsidemargin}
\put(-84.0,310.0){$ \leftarrow $}
\put(-22.0,290.0){$ \rightarrow $}
\put(398.0,300.0){Aussensteg}
\put(375.0,300.0){$ \leftarrow $}
\put(459.0,300.0){$ \rightarrow $}
\put(-55.0,-3.0){\line(1,0){10.0}}
\put(-65.0,-80.0){Fusssteg}
\put(-77.0,-90.0){Unterer Rand}
\put(-52.0,-55.0){$ \uparrow $}
\put(-52.0,-115.0){$ \downarrow $}
\put(-55.0,620.0){\line(1,0){10.0}}
\put(385.0,601.0){headsep}
\put(373.0,590.0){$ \uparrow $}
\put(373.0,612.0){$ \downarrow $}
\put(370.0,600.0){\line(1,0){10.0}}
\put(370.0,608.0){\line(1,0){10.0}}
\put(430.0,618.0){\line(1,0){10.0}}
\put(430.0,608.0){\line(1,0){10.0}}
\put(445.0,609.0){headheight}
\put(433.0,598.0){$ \uparrow $}
\put(433.0,622.0){$ \downarrow $}
\put(-65.0,666.0){topmargin}
\put(-52.0,685.0){$ \uparrow $}
\put(-52.0,647.0){$ \downarrow $}
\put(359.0,450.0){marginparsep}
\put(343.0,450.0){$ \leftarrow $}
\put(422.0,450.0){$ \rightarrow $}
\put(440.0,448.0){\line(0,1){10.0}}
\put(359.0,520.0){marginparwidth}
\put(348.0,520.0){$ \leftarrow $}
\put(429.0,520.0){$ \rightarrow $}
\put(440.0,518.0){\line(0,1){10.0}}
\put(347.0,518.0){\line(0,1){10.0}}
\put(359.0,482.0){marginparpush}
\put(347.0,482.0){$ \uparrow $}
\put(430.0,482.0){$ \downarrow $}
\put(385.0,-15.0){footskip}
\put(373.0,-29.0){$ \uparrow $}
\put(373.0,1.0){$ \downarrow $}
\put(370.0,-20.0){\line(1,0){10.0}}
\put(370.0,-3.0){\line(1,0){10.0}}
\put(445.0,-19.0){footheight}
\put(433.0,-29.0){$ \uparrow $}
\put(433.0,-6.0){$ \downarrow $}
\put(430.0,-20.0){\line(1,0){10.0}}
\put(430.0,-10.0){\line(1,0){10.0}}
\end{picture}
}
\end{document}
Marginalien Seite
Was Marginalien sind wurde ja bereits weiter oben beschrieben. Was uns nun noch fehlt ist die Möglichkeit die Marginalien in den anderen Seiten steg schreiben zu lassen, falls den dies gewünscht wäre.
Marginalien Rechts
Mit dem hier gezeigten Beispiel werden die Marginalien bei einem einseitigen Dokument in den rechten Ausensteg geschrieben.
\begin{document}
\marginpar{Rechts}
\end{document}
Marginalien Links
Mit dem hier gezeigten Beispiel und der Verwendung von reversemarginpar werden die Marginalien bei einem einseitigen Dokument in den linken Ausensteg geschrieben.
\begin{document}
\reversemarginpar
\marginpar{Links}
\end{document}
Marginalien bei Doppelseite
Bei der Verwendung von Doppelseiten werden die Marginalien immer in den Außensteg geschrieben. D.h. wenn ich in meiner Präambel twoside mit aufgenommen habe wie es beispielsweisse bei "Book" der Standart ist, so werden auf der ersten rechten Seite des Dokumentes doe Marginalien in den rechten Außensteg geschrieben und auf der Seite 2 d.h. der Rückseite der ersten Seite in den linken Außensteg. Somit sind die Marginalien immer im Außensteg vorhanden.
So kann zum Beispiel der twoside Eintrag in der Präambel aussehen.
\documentclass[a4paper,twoside,10pt]{article}
Die Marginalien werden bei der Verwendung von twoside weiterhin ganz normal mit dem Befehl \marginpar geschrieben.
Layout Vergleich
Da hier nun bereits öffter erwähnt wurde das es kleine Unterschiede bei den Layouts gibt, möchte ich diese gerne grafisch für ein besseres Verständniss darstellen:
Druck einseitig - US / EU Layout
Einseitig direkter Vergleich
Im direkten Vergleich ist der Grossenunterschied des Satzspiegels deutlich zu sehen. Beim EU Layout ist der Satzspiegel etwas breiter und der untere Fußsteg grösser als der Kopfsteg. Beim US Layout ist der gesamte Satzspiegel etwas schmaler, dafür sind die Stege oben/unten rechts/links gleich.
Druck beidseitig - US / EU Layout
Hier noch ein weiteres Beispiel für den beidseitigen Druck wie bei Büchern etc.
Beidseitig direkter Vergleich
Auch hier sind wieder im direkten Vergleich die Unterschiede von Höhe/Breite sowie den Stegen gut zu erkennen.
Automatische Satzspiegelkonstruktion
Wem also die amerikanischen LaTeX Standartlayouts nicht gefallen, kann diese mit den oben beschriebenden Dimensionsparamtern dementsprechend ändern. Da das ändern der gesamten Parameter eine knifflige Arbeit ist bei der das entsprechende Ergebniss am Ende dann doch nicht immer den eigenen Vorstellungen entspricht, gibt es eine einfachere Lösung die den Satzspiegel selbst berechnet und an die richtige Stelle platzieren zu lassen.
Das Zauberpacket nennt sich Typearea und stammt aus KOMA-Script.
KOMA-Script ist eine Sammlung von Dokumentenklassen ähnlich wie article, book usw. welche aber an den europäischen Raum und dessen Standarts angepasst wurden. Zu dieser Anpassung trägt typearea.sty seinen Teil bei, indem von ihm der Satzspiegel berechnet und dessen Prosition dementsprechend bestimmt wird. Somit fällt die ganze Handarbeit wie weiter oben beschrieben "festlegen der Abstände etc." weg. Typearea ist zwar bei den Standartklassen von LaTeX nicht dabei, kann aber dennoch bei ihrer Verwendung genutzt werden. D.h. nach der Installation von KOMA-Script oder Typearea müssen nicht unbedingt die KOMA-Script Klassen verwendet werden da typearea.sty auch in die Standartklassen mit als usepackage eingebunden werden kann.
Faktoren
Für die automatische erstellung kommen verschiedene Faktoren zusammen:
- Schriftgrösse
- Laufweite
- Schriftart
- Durchschuss
- Platz
- Wortlänge
Wichtig bei der Schrift ist ob diese eine Serifenlose Schrift oder eine Schrift mit Serifen ist, da durch Serifen die Zeilenwirkung verstärkt wird. Somit ist es für unser Auge einfacher den Wortern und Zeilen beim lesen besser zu vollgen. Fazit wäre das eine Zeile mit einer Serifenschrift somit länger sein dürfte als eine Zeile die mit Serifenloser Schrift geschrieben.
Beim Durchschuss ist es so, das hier ein etwas grösserer das lesen wesentlich erleichtern kann. Ein zu gross gewählter erschwärt es dagegen. Schaut man sich eine Seite mit zu grossem Durchschuss an, fällt auf das die Grauwerte gestört sind. In der Regel ist der LaTeX Standart so eingestellt das wir mit ca. 20% Durchschuss arbeiten.
Bei der Zeilenlänge kommt es ganz darauf an. Wenn wir alles in allem rechnen, d.h. mit Leerzeichen etc. kommen wir mit 60 bis 70 Zeichen pro Zeile auf einen recht guten Mittelwert.
Anwendung
Um Typearea verwenden zu können, benötigen wir einen kleinen Eintrag in unserer Präambel:
\usepackage[...]{typearea}
Hierbei müssen wir allerdings noch einen oder mehrere weitere Werte [...] Setzen welche im Anschluss kurz beschrieben werden.
BCOR - Wert
Der in obigem Beispiel noch fehlende Wert kann zum einen der BCOR Wert sein. Der BCOR Wert ist für die Bindekorrektur welche eventuell benötigt wird. Die Bindekorrektur benötigen wir da bei einer Bindung ein kleiner Teil unseres Steges ( Bundsteg ) verlohren geht und somit die Stege nicht mehr stimmen würden.
Ein Beispiel für eine Bindekorrektur kann so aussehen:
\usepackage[BCOR8.25mm]{typearea}
Was noch erwähnenswert bei der Bindekorrektur ist, das man pro Blatt ca. 0,75 mm zur Bindekorrektur dazu rechnen sollte, da beim Umschlagen einer Seite wenn diese zum Beispiel in einem Schnellhefter abgeheftet wurde durch den Falz oder Knick dieser Wert verlohren geht.
Wird auf eine Bindekorrektur verzichtet, so kann dieser Eintrag vollgendermassen aussehen:
\usepackage[BCOR0pt]{typearea}
DIV - Wert
Den DIV Faktor Wert benötigen wir um anzugeben in wie viele Streifen wir unsere Seite horizontal und vertikel für die Satzspiegelberechnung unterteilen möchten. Weiter oben haben wir ein Beispiel eines 9ner Rastersystemes gezeigt. Hier wäre für dieses Rastersystem [DIV9] richtig.
Da es zum grössten Teil auf die verwendete Schriftgrösse ankommen, so gibt es hier zu empfehlende Werte die ich keinem vorenthalten möchte.
Empfohlene Werte
Für DIN A4 bei einer Grundschriftgrösse:
- 10 pt = 8 DIV
- 11 pt = 10 DIV
- 12 pt = 12 DIV
In unserer Präambel könnte ein Eintrag so aussehen:
\usepackage[DIV8]{typearea}
Neuberechnung
Desweiteren haben wir sogar die Möglichkeit uns unseren Satzspiegel von Typearea ohne eine expliziete DIV Faktor Angabe berechnen zu lassen. Es wird also ein Satzspiegel mit einem guten DIV Wert berechnet. Für eine solche Berechnung verwenden wir vollgeden Eintrag in unserer Präambel:
\usepackage[DIVcalc]{typearea}
Möchte man wissen welcher als optimaler DIV Wert bei der Verwendung von Calc verwendet wurde, so reicht hier ein kleiner Blick in unsere *.log Datei. Hier sollte dann ein ähnlich wie hier gezeigter Eintrag zu finden sein:
DIV calculation for typearea with good linewidth. Package typearea Info: These are the values describing the layout: (typearea) DIV = 7
Mittelalterliche Kreisberechnung
Wir können uns den Satzspiegel sogar nach der mittelalterlichen Kreisberechnung von Typearea berechnen lassen:
\usepackage[DIVclassic]{typearea}
Anwendungsbeispiel
Hier nun ein vollständiges Anwendungsbeispiel:
\usepackage[BCOR12mm,DIV8]{typearea}
Satzspiegelmasse Übersicht
Für die entsprechenden DIV Werte die anzugeben sind, sind entsprechende Voreinstellungen für den Satzspiegel Stege etc. vorhanden.
Kleine Übersicht:
| DIV-Wert | Satzspiegel Breite | Satzspiegel Höhe | Kopfsteg | Außensteg | |
|---|---|---|---|---|---|
| 6 | 105,00 | 148,50 | 49,50 | 35,00 | |
| 7 | 120,00 | 169,71 | 42,43 | 30,00 | |
| 8 | 131,25 | 185,63 | 37,13 | 26,25 | |
| 9 | 140,00 | 198,00 | 33,00 | 23,33 | |
| 10 | 147,00 | 207,90 | 29,70 | 21,00 | |
| 11 | 152,73 | 216,00 | 27,00 | 19,09 | |
| 12 | 157,50 | 222,75 | 24,75 | 17,50 | |
| 13 | 161,54 | 228,46 | 22,85 | 16,15 | |
| 14 | 165,00 | 233,36 | 21,21 | 15,00 | |
| 15 | 168,00 | 237,60 | 19,80 | 14,00 |
Hierbei ist allerding zu sagen, das keine Bindekorrekturen verwendet wurden.
Die Werte in der hier dargestellten Tabelle, stammen aus "Die Anleitung - KOMA Script" welches auch unter Distributionen & Links hier im LaTeX Wiki Book aufgelistet und verlinkt ist.
Schriften
Bevor wir uns daran machen mit weiteren Schriften zu arbeiten als die welche uns unter LaTeX standartmäßig zu verfügung seteh, sollten wir uns ein bisschen Grundwissen über Schrift und Schriften aneignen.
Schriftbaum & Analyse
Bei uns hier im deutschen Kreis unterschieden wir hauptsächlich zwischen zwei Schriftarten:
- Gebrochene Schrift - ( Auch Fraktur genannt, allerdings nicht richtig )
- Antigua Schrift
Gebrochene Schrift
Die gebrochene Schrift wird auch oft als Fraktur bezeichnet was allerdings so nicht richtig ist. Der Begrif Gebrochene Schrift bezeichnet eine latainische Schrift bei der die Bögen der Schrift aus einer einzigen Schreibbewegung sind. Zudem sind bei der gebrochenen Schrift die einzelnen Bögen in den Buchstaben gebrochen was heissen soll das ein Richtungswechsel der Strichführung innerhalb eines Bogens vorhanden ist.
Bekannte gebrochene Schriften sind beispielsweisse:
- Schwabacher
- Initale
- Rotunda
Die Gebrochenen Schriften werden in weitere fünf Gruppen unterteilt laut DIN16518 welche insgesamt 14 Gruppen einteilt:
- Schwabacher
- Gotisch (Textura)
- Rundgotisch (Rotunda)
- Fraktur
- Fraktur-Varianten
Die anderen neun fehlenden Gruppen sind zum Teil sonstige oder auch andere welche zur Antigua gehören.
Antigua Schrift
Als Antigua wird eine Schriftart bezeichnet bei der die Bögen der einzelnen Buchstaben aus einem einzigen Schriftzug entstanden sind. Diese Bögen beinhalten keine Richtungsänderungen oder Richtungswechsel der Schreibform wie es etwa bei den Gebrochenen Schriften zu sehen ist. In der Westlichen Sprache sind die Antigua die wohl am meisten verwendete Druck- und Schreibschriften. So wie die Gebrochenen Schriften werden auch die Antigua in weitere Gruppen unterteilt.
- Venezianische Renaissance-Antiqua
- Französische Renaissance-Antiqua
- Barock-Antiqua
- Klassizistische Antiqua
- Serifenbetonte Linear-Antiqua
- Serifenlose Linear-Antiqua
- Antiqua-Varianten
- Schreibschriften
- Handschriftliche Antiqua
Serifen
Desweiteren wird unterschieden in Schriften mit und in Schriften ohne Serifen. Eine Serife ist ein Strich bei einem Buchstaben der quer zu seiner Grundline abschliesst. Durch diese kleinen Serifen bei den einzelnen Buchstaben wirkt der damit geschriebene Text so das es unserem Auge beim lesen leichter fällt der Linie bzw. Zeile welche wir gerade lesen zu vollgen. Wenn eine Serifen Schrift verwendet wird, kann die eigentliche Zeilenlänge mit ihrer Zeichenanzahl etwas länger sein. Sollte aber dennoch nicht über 70 Zeichen kommen. Alle Zeilen mit mehr als 70 Zeichen einschliesslich den Leerzeichen sind selbst für geübte leser nicht mehr angenehm zu lesen. Serfien sind durch die betonung der Grundlinie sowie der Mitellinie besonders bei grösseren Texten geeignet.
Grund- und Mittellinie
Zur besseren Verdeutlichung hier eine Abbildung welche die Grund- und Mittellinie zeigt.
Quellcode:
\begin{document}
\begin{picture}(300,300)
\put(-35.0,36.0){\line(1,0){250}}
\put(-35.0,25.0){\line(1,0){250}}
\put(-38.0,38.0){$ \downarrow $}
\begin{scriptsize}
\put(-37.0,46.0){Mittellinie}
\end{scriptsize}
\put(-38.0,18.0){$ \uparrow $}
\begin{scriptsize}
\put(-37.0,10.0){Grundlinie}
\end{scriptsize}
\begin{Huge}
\put(0.0,25.0){Super Linux Club}
\end{Huge}
\end{picture}
\end{document}
Schriftfamilie
Unter dem Namen Schriftfamilie verseht man alle Varianten eines Schriftbildes einer Schrift. Eine Schriftfamilie wäre beispielsweisse Computer Modern Roman da diese weitere Schriftschnitte enthält.
Schriftschnitte
Als Schriftschnitt wird auch der Schriftstiel bezeichnet. Dieser enthält verschiedene Varianten einer Schriftfamilie wie zum Beispiel:
- Schriftstärke
- Schriftdicke
- Schriftlage
Als dekoratieve Schriftschnitte könne auch:
- Kapitälchen
- Initalen
- Mediävalziffern
- Bruchziffern
- Ligaturen
zählen.
Schriftgrad
Als Schriftgrad wird auch das Schriftsatzmaß bezeichnet das in weitere Punkte unterteilt wird.
- Konsultationsgröße
- Lesegröße
- Schaugröße
Konsultationsgröße
Als Konsulationsgröße wird eine Schrift mit 3 bis 9 Didot-Punkten bezeichnet.
Lesegröße
Als Lesegröße wird eine Schrift mit 10 bis 13 Didot-Punkten bezeichnet. Daher wird bei den meisten texten diese als Ideale Grundschriftgröße gesehen.
Schaugröße
Als Schaugröße wird eine Schrift mit 14 bis 47 Didot-Punkten bezeichnet
Schriftgrad - Fußnoten & Marginalien
Der Schriftgrad von Fußnoten und Marginalien ist in der Regel 2 bis 5 Didot-Punkte kleiner als die Grundschrift. Wird also eine Grundschrift von 10 Didot-Punkten verwendet, so haben die Fußnoten, Marginalien eine Größe von 5 bis 8 Didot-Punkten.
Schrift Qualität
In der EDV werden verschiedene Schriften in unterschiedlichen Dateiformaten zu verfügung gestellt. Die zwei bekanntesten und auch weit verbreitetsten sind die TrueType Schriften und die welche im PostScript Format vorliegen. Vorgestellt wurde TrueType im Jahr 1991 von der Firma Apple Inc. und lizenziert von Microsoft Corporation. Integriert sind diese in den Betriebsystemen Windows und MacOS. Unter Linux und anderen Unix Systemen ist es unter FreeType verfügbar.
Die TrueType Schriften werden mit dem selben Prinzip wie die Vektorgrafiken aufgebaut, d.h. aus Konturen.
PostScript wird seit 1984 von Adobe entwikelt und unterscheidet sich am stärksten von den TrueType Schriften in den Kurven.
Bei TrueType Schriften werden Bézierkurven der zweiten Ordnung verwendet, bei PostScript Schriften Bézierkurven der dritten Ordnung. Hier durch ist die Qualität der PostScript Schriften im allgemeinen höher als die der TrueType Schriften.
Weitere Schriften
Unter LaTeX haben wir die Möglichkeit viele weitere Schriften verwenden zu können, ich möchte zeigen wie es geht. Zu aller erst, ist es wichtig zu sagen das die Art und Weise die wir bereits in den Grundlagen kennengelernt haben um eine Schrift auszuwählen hier etwas anderst funktioniert. Wir haben ein paar Punkte die ich kurz nennen möchte, da diese für die Auswahl oder Bestimmung unserer gewünschten Schrift benötigt werden.
Schriftatribute:
- Fontencoding
- Fontfamily
- Fontseries
- Fontshape
- Fontsize
Fontencoding: Hiermit wird der gewünschte Zeichensatz angegeben.
Fontfamily: Damit wird unsere Schriftfamilie ausgewählt.
Fontseries: Wird für die Schriftstärke benötigt.
Fontshape: Benötigen wir um zu bestimmen ob wir eine aufrechte oder geneigte Form möchten.
Fontsize: Dint zur Grössenbestimmung der Schrift und dessen Zeilenabstand oder Durchschuss.
Sehr wichtig zu erwähnen ist hier das man eventuell diverse Pakete mit weiteren Schriften installieren muss um diese nutzen zu können. Dazu kommt nocht das nicht immer alle Schriften in allen Grössen etc. verfügbar sein können.
Fontencoding - Zeichensatz
Mit Zeichensatz wird eine Sammlung von diversen Zeichen bezeichnet. Dies können Buchstaben wie auch Mathematische oder Sonderzeichen sein.
Fontfamily - Schriftfamilie
Unter der Bezeichnung Schriftfamilie versteht man eine Gruppe von Schriftstielen welche gemeinsame Merkmale in ihrer Form aufweissen. Eine Schriftfamilie kann also aus vielen einzelnen Schriften bestehen, welche wiederum als Schriftfamilie in verschiedene Klassifikationen oder auch Schriftsippen als Familie zugeordnet werden können. Eine unter LaTeX verfügbare Schriftfamilie wäre beispielsweisse die Computer Modern Roman.
Fontseries - Schriftstärke
Mit der Schriftstärke wird die Dicke der Schrift oder deren Stärke, Fette bezeichnet. Die genaue Bezeichnung der Schrift, ob diese nun dick oder nicht ist steht dem Hersteller der Schrift frei. Leider funktioniert hirdurch die Einteilung in die Schriftstärkenklassen nicht so gut wie man es gerne hätte, da all dies eine reine Geschmacksache ist. Sehr oft werden hier die Bezeichnungen durcheinander geworfen so das Schriften mit der gleichen Stärke unterschiedlich zugeordnet und benannt werden.
Schriftstärken
- Ultraleicht = Ultra Light, Ultra Thin
- Extraleicht = Extra Light, Fein, Thin
- Leicht = Light, Light Plain
- Halbleicht = Semi Light, Mager, Semi Light Plain
- Normal = Regular, Buch, Werk, Book, Medium, Plain, Roman
- Halbfett = Semi Bold, Kräftig)
- Fett = Bold, Dreiviertelfett, Demi, Heavy
- Extrafett = Extra Bold, Black
- Ultrafett = Ultra Bold, Extra Black, Ultra
Schriftdicke
Unter der Schriftdicke versteht man die Breite der Buchstaben.
- Ultraschmal = Ultra Condensed
- Extraschmal = Extra Condensed
- Schmal = Condensed, Compressed, Narrow
- Halbschmal =Semi Condensed
- Normal = Regular
- Halbbreit = Semi Expanded
- Breit = Expanded, Extended)
- Extrabreit = Extra Expanded
- Ultrabreit = Ultra Expanded
Fontshape - Schriftlage
Mit Schriftlage geben wir an ob wir eine Kursive, Schräggestellte oder Aufrechte Schrift möchten.
Schriftlage
- Normal = Aufrecht, upright
- Kursiv
- Italic, oblique = Echte Kursive
- slanted, sloped roman = Unechte Kursive
- Echte Kursive = Hier wurde die Schrift vom Desinger entworfen.
- Unechte Kursive = Die Schrift wurde mit Hilfe von Software einfach schräg gestellt.
Fontsize - Schriftgrösse
Unter Fontsize versteht man die Schriftgrösse welche in der Regel in (pt) = Punktgrösse angegeben ist. Eine 12pt Schrift ist in etwa das was man von einer Schreibmaschiene her kennt.
In der Regel stehen einem vollgende Grössen zu verfügung:
5, 6, 7, 8, 9, 10, 10.95, 12, 14.4, 17.28, 20.48, 24.88
Desweiteren kann mit dem Befehl für die Schriftgrösse zudem der Zeilenabstand ( Durchschuss ) in (pt) Punktgrösse mit angegeben werden.
Schriften Installieren
Um unter LaTeX weitere Schriften verwenden zu können, müssen diese erst installiert werden. Für die Installation sollte man zuerst schauen ob nicht vl. der Distributor bereits fertige Binäre Pakete zur Installation für seine jeweilige Distribution anbietet welche weitere Schriften für LaTeX enthalten. Da ich selbst nicht jede Distribution kenne und im Einsatz habe, kann ich hier nur einen einfachen weg zeigen um unter meiner verwendeten Distribution weitere Schriften zu installieren.
Tipp: Debian
Stand: 07/2007
Unter Debian gibt es derzeit das Paket texlive-fonts-extra für das TexLive System welches weitere Schriften etc. enthällt.
Ansonsten besteht die Möglichkeit sich die einzelnen dementsprechenden Pakete bei CTAN zu besorgen.
Für deren Installation sollte man die jeweils zugehörige Hilfedateien lesen.
Im Anschluss wird hier nun beschrieben wie den eine Installierte Schrift unter LaTeX verwendet werden kann.
Schriften Laden
Wenn weitere Schriften installiert wurden, müssen wir diese zuerst auswählen um sie verwenden zu können. Zum einen kann es nötig sein das vor der Verwendung erst ein weiteres Paket mit in die Präambel geschrieben werden muss um dieses laden zu können. Eine Sehr bekannte Schrift wäre beispielsweisse die Schwabacher Schrift. Soll diese nach deren Installation unter LaTeX in einem Dokument verwendet werden, muss sie zuvor als Paket mit in die Präambel geschrieben werden. Hier ein Beispiel dazu:
\usepackage{oldgerm}
Welcher Style Name in diesem Fall oldgerm mit in die Präambel zu schreiben ist, muss der dazugehörigen Dokumentation des installierten Paketes entnommen werden.
Schrift Auswählen
Haben wir den entsprechenden Befehl in unsere Präambel für das laden des Paketes geschrieben, so können wir unsere neue Schrift schliesslich verwenden. Was uns nun noch fehlt ist die genaue Angabe was wir den überhaupt verwenden wollen. Hierzu gibt es ein paar Befehle:
- \fontencoding{}
- \fontfamily{}
- \fontseries{}
- \fontshape{}
- \fontsize{}{}
- \selectfont
fontencoding
Hiermit kann der entsprechende Zeichensatz gewählt werden.
\fontencoding{U}
Das U steht hier für UTF-8, welche Angaben möglich sind muss der Dokumentation des installierten Schriftpaketes entnommen werden.
fontfamily
Hiermit wird die Familie ausgewählt.
\fontfamily{cmr}
Angenommen ich möchte die Computer Modern Roman Schrift verwenden, so lese ich deren Dokumentation in dieser beschrieben ist das für deren Auswahl CMR als Fontfamilie anzugeben ist.
fontseries
Bei diesem Befehl wir die fontseries angegeben, ich möchte gerne bold extendet verwenden und schau in die Doku wo mir gesagt wird das hierzu bx anzugeben ist.
\fontseries{bx}
fontshape
Zu guterletzt wünsche ich mir als Schriftlage eine Kursive und schaue wieder in der Doku nach was hierfür falls vorhanden angegeben werden muss.
\fontshape{it}
fontsize
Die Schriftgrösse und der Zeilenabstand kann ebenfalls mit angegeben werden, als Beispiel wähle ich hier eine Grösse von 24,88 pt und einen Zeilenabstand bzw. Durchschuss von 5 pt.
\fontsize{24.88}{5}
selectfont
Selectfont ist ein Operator zum festlegen von Fonts und Schriftgrössen.
\selectfont
Beispiel - Computer Modern Roman
Ich möchgte hier noch schnell ein fertiges Beispiel Zeigen. Da die Computer Modern als Standart Schriftfamilie unter LaTeX verwendet wird ist mein Beispiel auf diese Schrift bezogen da sie jeder in seinem LaTeX System hat und so die verschiedenen Paramter probieren und testen kann, ohne zuerst irgend welche weiteren Schrifften runterladen und installieren zu müssen.
\begin{document}
\fontfamily{cmr} \fontseries{bx} \fontshape{it} \fontsize{14.4}{3} \selectfont
Computer Modern Roman bold extended italic
\end{document}
Schrift Paket
Es gibt derzeit ein Bündel von div. Schriften welches sich psnfss nennt und absolut zu empfehlen ist. Verfügbar ist es auf den CTAN Servern zum downloaden und anschliessenden installieren. Dieses Bündel ist AFAIK bei einer eueren LaTeX Version bereits dabei und beinhaltet mehrere diverse Schriften die ich im Anschluss kurz vorstellen möchte.
Tipp: Debian
Stand: 07/2007
Unter Debian befindet sich dieses Paket in texlive-latex-base und kann bequem via APT installiert werden.
Bevor wird die Schriften verwenden, sollte ein entsprechender Eintrag in die Präambel des Dokumentes geschrieben werden.
\usepackage[T1]{fontenc}
\usepackage{textcomp}
Durch die Angabe von T1 fontenc stellt die Font-Kodierung auf ein neueres Format um, das besser mit Umlauten funktioniert.
Das Paket textcomp lädt in LaTeX die TC-Schrifften für viele weiter Zeichen wie das Copyright oder Copyleft wie auch das Euro Symbol. Zudem alle Sonderzeichen aus ISO 8859-1.
Helvetica
Helvetice ist der Name einer Schriftart welcher weltweit geschützt ist und der Firma Linotype gehört. Sie ist eine Serifenlose Linearantiquare Schrift mit klassizistischem Charakter welche 1957 vom Grafiker Max Miedinger und Eduard Hoffmann entwikelt wurde. Ihr erster ursprünglicher Name war "Neue Haas-Grotesk" da Eduard Hoffmann der Geschäftsführer von der Haas'schen Schriftgiesserei AG war. Nach einer Übernahme von der D. Stempel AG bekamm die Schrift 1961 ihren Namen Helvetica unter dem sie Welt bekannt wurde. Im Jahre 1985 ist es zu einer weiteren Übernahme von Linotype gekommen.
Ein freier OpenSource Ersatz für Helvetica ist die "Nimbus Sans L Regular" Schrift welche von URW Software & Type kostenlos zu Verfügung gestellt wird.
\fontfamily{phv} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{m} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{phv} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{b} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{b} \fontshape{sc} \selectfont
\fontfamily{phv} \fontseries{mc} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{mc} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{mc} \fontshape{sc} \selectfont
\fontfamily{phv} \fontseries{bc} \fontshape{n} \selectfont
\fontfamily{phv} \fontseries{bc} \fontshape{sl} \selectfont
\fontfamily{phv} \fontseries{bc} \fontshape{sc} \selectfont
Avant Garde
Die Avent Garde sollte zuerst überhaupt keine Schrift werden, sie ist der Name oder das Loge eines US-Kulturmagazines namens Avant Garde. Der Herrausgeber Ralph Ginzburg und Herb Lubalin suchten zu dem Namen dieses Magazienes eine einzigartige Schrift welche nach viel eigenem Testen und probieren am Ende Herbert F. Lubalin (1918 ? 1981) entworfen hatte. Die Avant Garde Schrift ist nicht für große Texte, d.h. den Mengen Satz geeignet. Am meisten wurde sie bisher in Werbung eingesetzt. Der bekanntetste Konzern welcher sie in einer Werbung 1975 verwendete war die Marke Addidas, zudem ist sie auf div. CD Covern zufinden. Im grossen und ganzen ist sie am besten für Titel oder Überschrifften geeignet. Auf Visitenkarten oder Briefköpfen würde sie sich bestimmt auch ganz gut machen.
\fontfamily{pag} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pag} \fontseries{m} \fontshape{sl} \selectfont
\fontfamily{pag} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pag} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pag} \fontseries{b} \fontshape{sl} \selectfont
\fontfamily{pag} \fontseries{b} \fontshape{sc} \selectfont
Bookman
Die Bookman Schrift wurde von Alexander Phemister im Jahr 1860 entwikelt. Es ist eine Serifen Schrift die eigentlich für die Verwendung in Büchern gedacht ist. Die sehr Populäre ITC Bookman stammt von ihr ab und wurde 1975 von Ed Benguiat designed .
\fontfamily{pbk} \fontseries{l} \fontshape{n} \selectfont
\fontfamily{pbk} \fontseries{l} \fontshape{it} \selectfont
\fontfamily{pbk} \fontseries{l} \fontshape{sc} \selectfont
\fontfamily{pbk} \fontseries{db} \fontshape{n} \selectfont
\fontfamily{pbk} \fontseries{db} \fontshape{it} \selectfont
\fontfamily{pbk} \fontseries{db} \fontshape{sc} \selectfont
Charter
Die Charter Schrift wurde von einem der bekanntesten Schriftsteller "Matthew Carter" im Jahr 1987 ins Leben gerufen. Er ist der Sohn des ebenfalls berühmnten Typografen Harry Carter. Matthew Carter zählt zu den bekanntesten der Computer Schriften Macher neben Hermann Zapf, Adrian Frutiger oder Erik Spiekermann. Desweiteren stammem weitere Schriften wie die Helvetica Compressed oder Shelly sowie Snell und Verdana von ihm.
\fontfamily{bch} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{bch} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{bch} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{bch} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{bch} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{bch} \fontseries{b} \fontshape{sc} \selectfont
Courier
Bei Courier handelt es sich um eine von Howard Kettler im Jahre 1956 entwikelte Schrift für Schreibmaschienen und Computer. Es ist wie bei Schreibmaschienen üblich, eine nicht proportionale Schrift mit sehr sarken Serifen. Verwendet werden die nicht proportionalen Schriften meist bei eMails, Programiersprachen und Computerterminales da sie über eine feste Zeichenbreite verfügen.
\fontfamily{pcr} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pcr} \fontseries{m} \fontshape{sl} \selectfont
\fontfamily{pcr} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pcr} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pcr} \fontseries{b} \fontshape{sl} \selectfont
\fontfamily{pcr} \fontseries{b} \fontshape{sc} \selectfont
New Century Schoolbook
Century Schoolbook wurde 1919 von Morris Fuller Benton entworfen welcher ein in den USA bekannter Typograf und Ingenieur war (1872–1948). Weitere von ihm recht bekannte Schriften sind Bodoni-Antiqua, Broadway, Century, Franklin Gothic, Clearface, Celtenham, und Stymie. Century Schoolnook ist ein etwas älterer Stiel mit Serifen welche für Schulbücher gedacht war und bei diesen auch verwendet wurde.
\fontfamily{pnc} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pnc} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{pnc} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pnc} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pnc} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{pnc} \fontseries{b} \fontshape{sc} \selectfont
Palatino
Die Palatino Schrift ist eine Französische Renaissance-Antiqua welche von Hermann Zapf im Jahre 1948 erfunden wurde. Diese Schrift wurde in der Nachkriegszeit Old-Style aus Deutschland geschaffen um auch auf minderwertigem Papier ein gutes Bild zu machen.
\fontfamily{ppl} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{ppl} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{ppl} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{ppl} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{ppl} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{ppl} \fontseries{b} \fontshape{sc} \selectfont
\fontfamily{pplx} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pplx} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{pplx} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pplx} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pplx} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{pplj} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{pplj} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{pplj} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{pplj} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{pplj} \fontseries{b} \fontshape{it} \selectfont
In diesen Beispielen sehen ein paar Schriften doch fast gleich aus, man könnte meinen sie wären doppelt gelistet was natürlich nicht stimmt. Wir haben hier zum Teil drei unterschiedliche Schrift Familien welche nur sehr kleine aber feine Unterschiede aufweissen.
- ppl
- pplx
- pplj
Bei sehr genauem Hinsehen erkennen wir die kleinen Unterschiede.
\fontfamily{pplj} \fontseries{m} \fontshape{n} \selectfont
Palatino Medium Normal
\fontfamily{pplx} \fontseries{m} \fontshape{n} \selectfont
Palatino Medium Normal
\fontfamily{ppl} \fontseries{m} \fontshape{n} \selectfont
Palatino Medium Normal
Times
Die Times ist eine von Stanley Morison und Victor Lardent im Jahre 1931 entwikelte Barock-Antiqua-Schrift. Von der ursprünglichen Times existieren im heutigen Computerzeitalter viele verschiedene Versionen wie beispielsweise die Times New Roman welche nicht gleich Times ist ! Dem Computerzeitalter hat es die Times zu verdanken das sie so populär geworden ist, Fimren wie Apple Adobe oder Microsoft haben zum grossen Teil dazu beigetragen. Was die genaue Entstehung der Times Schrift angeht, so gibt es hier anscheinend verschidene Versionen. Man ist sich aber dennoch einig, das die Times für die Londoner Zeitung "The Times" entworfen wurde. Die Times New Roman wurde auf Wunsch von Microsoft eingeführt und von Monotypes entwickelt welche von der Times New Roman TS abstammt. Sie wurde damals extra an die deutschen Texte angepasst, da wir hier sehr viele Großbuchstaben in unserer Rechtscheibung verwenden im Vergleich zum Englischen.
Seit dem Jahre 2004 ist es in den USA Gesetzt alle Diplomatischen Arbeiten in der Times New Roman mit 14pt zu schreiben, anstelle der verherigen Courier New in 12pt.
Unter den Unix Systemen findet sich hier die "Nimbus Roman No9 L" von URW welche als Public Domain PostScripc Version der Times Roman freigegeben wurde. MacOS kommt mit der von Linotypes "Times Roman" und Microsoft mit der an Monotypes in Auftrag gegebener "Times New Roman".
Unter LaTeX schreiben wir in den hier vollgenden zur Times gezeigten Beispielen mit der richtigen originalen Times und nicht mit der Times New Roman.
\fontfamily{ptm} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{ptm} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{ptm} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{ptm} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{ptm} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{ptm} \fontseries{b} \fontshape{sc} \selectfont
Zapf Chancery
ermann Zapf der damalige Direktor der Stempel AG liebte die Kalligraphie, die Kunst des schön Schreibens. 1977 ging er als Professor an die Rochester Fachhochschule für Technologie in New York und entwar dort die Schriftkegel für Palatino, Optima, Zapf ( Chancery - im Jahre 1979 ) und Zapf Dingbats. Die Chancery ist Schulschrift, Englische Schreibschrift, Künstlerschreibschrift sowie für den Mengentext in machen Kinder Büchern geeignet.
\fontfamily{pzc} \fontseries{mb} \fontshape{it} \selectfont
Utopia
Die Utopia Schrift stammt aus dem Jahre 1989 und wurde designet von Robert Slimbach. Das großste und wohl bekannteste Beispiel zu dieser Schrift ist die Berliner Zeitung welche sie als Ausschrift nutzt. Ein kleiner Bericht vom 20.05.2005 über die Utopia in der Berliner Zeitung - online.
\fontfamily{put} \fontseries{m} \fontshape{n} \selectfont
\fontfamily{put} \fontseries{m} \fontshape{it} \selectfont
\fontfamily{put} \fontseries{m} \fontshape{sc} \selectfont
\fontfamily{put} \fontseries{b} \fontshape{n} \selectfont
\fontfamily{put} \fontseries{b} \fontshape{it} \selectfont
\fontfamily{put} \fontseries{b} \fontshape{sc} \selectfont
Eigene Schriften
Wer sich selbst einmal Schriften zugelegt hat für die er bezahlen musste, kann selbst diese unter LaTeX verwenden. Was allerdings dazu gesagt werden muss, das es nicht ganz einfach ist. Eventuell jeh nach dem in welchem Format diese Forliegen, müssen diese umgewandelt werden. So kann zum Beispiel eine Schrift im OpenType Format mit Hilfe von cfftot1 ins *.pfb Format converteirt bzw. umgewandelt werden.
Ich habe die ganze Geschichte ein einziges mal mit meiner Liblingsschrift der Sabon von Jan Tschichold gemacht, welche ich ebenfalls im OpenType Format vorliegen hatte. Das Umwandeln habe ich mit einem kleinen ShellScript bewerkstelligt.
#!/bin/sh mkdir -p pfb echo "Creating PostScript fonts ..." for font in otf/*.otf do base=$(basename "$font" .otf) cfftot1 "$font" "pfb/$base.pfb" done
Autor mit weiteren Infos zur Umsetzung sind hier zu finden.
The LaTeX Font Catalogue.
Font Guid PDF. ![]()
Für TrueType Font unter LaTeX (1/2)
Für TrueType Font unter LaTeX (2/2)
Hier das fertige Ergebnis in Sabon Italic, Sabon Medium und Sabon Kapitälchen.
Beste Schrift
Welche ist die beste Schrift überhaupt ?
Die beste Schrift überhaupt gibt es nicht, da es immer auf das ankommt was man letstenendes damit machen möchte. Die wohl belibtetste Schrift überhaupt wird Helvetica sein. Die Schrift Futura war zum Beispiele eine der populärsten überhaupt im 20. Jahrhundert. Welche Schrift aber die schönste ist, muss jeder für sich selbst entscheiden. Ich selbst verwende als Grundschrifftart bei all meinen Dokumenten die Standart LaTeX Schriffamilie Computer Modern, da diese nicht linear skaliert werden muss weil sie in vielen Grössen zu verfügung steht. Desweiteren wurde sie vom macher des TeX Systemes Donald E. Knuth entwikelt. Ich nehme daher einfach mal an, das eine von Knuth entwikelte Schrift mit Sicherheit nicht die schlechteste ist. Zudem gefällt mir noch die Schrift Sabon, welche vom Grossen Meister der neuen Typografie Jan Tschichold stammt.
Arial ist eine Schrift die von Robin Nicholas und Patricia Saunders entwikelt wurde. Da diese seit Windows 3.1 von MS mitgeliefert wird, ist es eine der am weitesten verbreiteten Schriften überhaupt. Arial ist eine Art leicht abgewandelte Helvetica mit nur recht kleinen Unterschiden, daher stehen Typografen dieser Schrieft doch recht skeptisch gegenüber. Bei Times New Roman ist es so ähnlich, sie wurde von Stanley Morison und Victor Lardent entworfen und hat ebenfalls ihre Bekanntheit der Firma Microsoft wie auch Apple und Adobe zu verdanken. Anscheinen konnte oder wollte Microsoft keine teuren Profi Schriften bei Windows oder ihrem MS-Office Paket mitliefern, was somit auch der Grund ist weshalb sich diese so hartnäckig halten. Zudem ist es vl. erwähnenswert zu sagen das die Times New Roman extra für den deutschen Raum angepasst wurde, da wir in unserer deutschen Rechtschreibung doch recht viele Grossbuchstaben im vergleich zu anderen wie Englischen verwenden. Die Times New Roman eignet sich daher nicht für jede Sprache.
Ohne andere Schriften schlecht reden zu wollen, muss gesagt werden das die LaTeX Standart Schrift wirklich eine gute Wahl ist. Es wurde hier einen großen Wert auf die Ästethik und die Funktionalität gelegt. Sie kann sich daher problemlos mit den Windows Pendanten oder sehr teuren Profi Schriftfamilien Messen lassen. Zudem ist es bei den Windows meist TrueType-Fonts so, das dessen Buchstaben bei den einzelnen Schriftgraden vergrössert oder verkleinert werden. Hierdurch erkennen sogar nicht Profies deutliche Defizite was bei der LaTeX Standartschriftfamilie nicht ist.
Welche Schriftklassifikation
Wir sollten in unserer heutigen Zeit als Schrift eine Antiqua Schrift verwenden. Denn die Antiqua Schrift ist eine Schrift unserer Zeit in der wir uns befinden. Wir sollten keine Fraktur mehr in unseren Texten verwenden und somit versuchen die für die damalig sehr gute Typografie nach zu äffen. Die Frakturen waren zu ihrer Zeit genau richtig, gehören allerdings nicht mehr in unsere Zeit. Wenn wir heutige Texte besser darstellen und gestallten wollen wie die damaligen, so können wir dies also nicht mit der Fraktur von damals schaffen, sondern müssen neue Dinge welche der heutigen Zeit entsprechen verwenden und mit hilfe dieser versuchen besser zu sein als die damaligen. Schwabacher ist eine sehr gute, wunderschöne Schrift, aber in der heutigen Zeit absolut fehl am Platz. In den damaligen Texten war sie genau passend, aber dies eben nur zur damaligen Zeit. Wir benötigen eine natürliche, einfache, gut leserliche und leichte Schrift, aber anscheinend ist dies noch nicht bis zu jedem durchgedrungen. Oder aus welchem Grunde wird zum Beispiel an Bahnhöfen der Stationsnahme noch so oft in Fraktur anstelle in Lateinischer Schrift geschrieben ? So fällt es anderen Ländern bzw. Völkern die bei uns zu Besuch oder auf der Durchreise sind noch schwerer diese Wörter zu entzifern.
Toller Fortschritt den wir da haben !
Mehr Mathematisches
Plotten von Funktionen mit PSTricks
Ein paar wichtige Dinge
Der erste Fehler
Den ersten Fehler macht man, wenn man seinen Quellcode pstricks.tex nennt. Das ist nämlich schon der Name des PSTricks-Paketes. Und deshalb erntet man Fehlermeldungen.
PSTricks auf dem Bildschirm betrachten - PDF erstellen
Leider kann der DVI-Betrachter viele Dinge nicht richtig darstellen! Wenn man seine Plotts richtig dargestellt haben möchte, dann muß man mindestens eine Postsciptdatei erstellen. Wenn man ein PDF haben möchte, dann kann man die Postscriptdatei mit ps2pdf in ein PDF umwandeln. Es funktioniert nicht, wenn man die DVI-Datei in ein PDF umwandeln will.
Allgemeine Parameter
Notwendige Pakete
Es ist völlig ausreichend, das Paket pst-3dplot zu laden. Falls man nur 2-D-Plotts zu Papier bringen will, dann reicht auch das Paket pst-plot. Für alle Beispiele hier in diesem Artikel reicht es, diese Zeile in die Präambel zu schreiben:
\usepackage{pst-3dplot}
Die Umgebung
PSTricks stellt eine Umgebung bereit, in die man plotten kann. Diese Umgebung reserviert Platz für den Plott auf dem Papier. Hier die Umgebung:
\begin{pspicture}[Grundlinie](x0,y0)(x1,y1)
Plott
\end{pspicture}
- (x0,y0) gibt die linke untere Ecke an, (x1,y1) gibt die rechte obere Ecke an.
- Der Parameter "Grundlinie" ist eine Zahl zwischen 0 und 1. Dieser Parameter steht per default auf 0. Falls man neben seinem Bild noch etwas schreiben möchte, empfiehlt es sich, diesen Parameter auf 0.5 zu setzen. Das sieht schön aus, ist aber Geschmacksache.
Um seinen Plott einzurahmen, gibt es den Befehl
\psframe[Parameterliste](x0,y0)(x1,y1)
Mit den optionalen Parametern kann man etwa die Linienstärke bestimmen. Die Defaulteinstellungen sind allerdings OK. Man kann die Parameter also einfach weglassen. Für (x0,y0)(x1,y1) setzt man am besten die gleichen Werte ein, wie für das pspicture.
Manchmal kann es passieren, das man über das Bild hinausplottet. Dann möchte man abschneiden, was über den Rahmen hinausragt. Dafür gibt es 2 Möglichkeiten:
1. Clipping:
\psclip{Irgendein Rahmen}
\endpsclip
Als Rahmen setzt man dann seinen psframe ein.
2. Die Sternchenversion von pspicture.
\begin{pspicture}*[Grundlinie](x0,y0)(x1,y1)
Plott
\end{pspicture}
Beide Versionen schneiden ab, was vielleicht über den Rand des Bildes ragt. Clipping funktioniert auch mit anderen Objekten. Auch innerhalb des Bildes. Damit ist unsere Umgebung fertig. Hier ist sie:
Die vollständige Umgebung
\begin{pspicture}[Grundlinie](x0,y0)(x1,y1)
\psclip{\psframe[Parameterliste](x0,y0)(x1,y1)}
Hier
wird
geplottet.
\endpsclip
\end{pspicture}
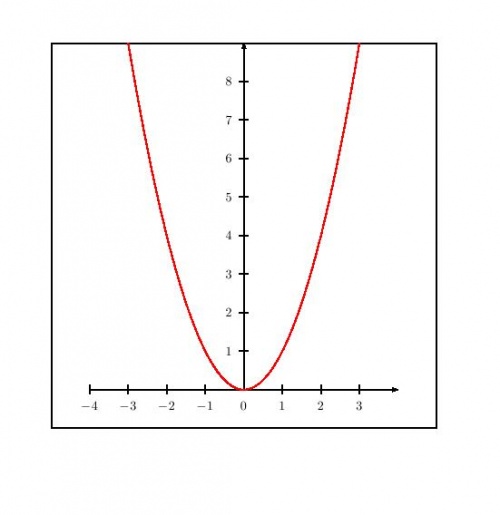
Diese vollständige Umgebung habe ich gleich im ersten Beispiel f(x)=x² benutzt. In den weiteren Beispielen habe ich auf den Rahmen und auf Clipping verzichtet.
Skalieren der Plotts
Es gibt mehrere Möglichkeiten, einen Plott zu vergrößern:
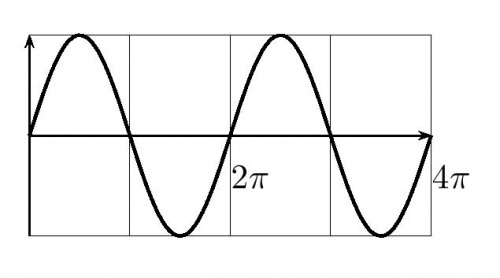
- Der Befehl \scalebox{Vergrößerung}{pspicture}. Das wird im Beispiel Sinusfunktion demonstriert.
- Man ändert die Längeneinheiten mit dem Befehl \psset{unit=1cm}. Unit=1cm ist die Defaulteinstellung. Ändert man diese auf unit=2cm, wird der Plott doppelt so groß. Interessant wird diese Möglichkeit, weil man mit dem Kommando \psset{xunit=1cm, yunit=1cm} die einzelnen Achsen unterschiedlich vergrößern oder verkleinern kann. Leider wirkt sich dieser Befehl nur auf die PSTricks-Objekte aus. Alle anderen Objekte, welche man in seinem pspicture plaziert, werden nicht vergrößert. Sie ändern nicht einmal ihre Lage im Bild. Mit dem Befehl \psset{unit=2cm} wurde das Beispiel "Sinusfunktion in der Ebene" vergrößert.
2-D-Plotts
Das Koordinatensystem
Um das Koordinatensystem darzustellen, gibt es den Befehl:
\psaxes[optionale Parameter]{->}(0,0)(x1,y1)(x2,y2)
- x1 gibt die linke Seite der x-Achse an
- x2 gibt die rechte Seite der x-Achse an
- y1 gibt die untere Seite der y-Achse an
- y2 gibt die obere Seite der y-Achse an.
Folgende Parameter sind vielleicht interessant:
- labels=all / x / y / none Die Defaulteinstellung ist all. Aber speziell in Verbindung mit dem \psgrid möchte man vielleicht keine Beschriftung haben. Dann setzt man labels=none.
- ticks=all / x / y / none Die Defaulteinstellung ist all.
- linewidth=dim In Verbindung mit dem \psgrid möchte man vielleicht dickere Achsen zeichen. Man könnte etwa linewidth=1pt wählen.
Die Parameter werden durch ein Komma, voneinander getrennt.
Das Gitternetz \psgrid
Das Gitternetz zeichnet man mit folgendem Befehl:
\psgrid[Parameter](0,0)(x1,y1)(x2,y2)
Mögliche Parameter:
- (x1,y1): sind die Koordinaten der linken unteren Ecke.
- (x2,y2): sind die Koordinaten der rechten oberen Ecke.
- gridwidth gibt die Dicke des Zeichenstiftes an. Ich habe sie im Beispiel etwas feiner auf 0.1pt gestellt.
- gridlabels gibt die Größe der Beschriftung an. Falls man keine Beschriftung wünscht, gibt man gridlabels=0pt an.
- subgriddiv=Anzahl Mit subgriddiv kann man das Gitternetz weiter unterteilen. Je größer die Anzahl, um so feiner ist die Unterteilung.
- griddots=Anzahl Wird dieser Parameter angegeben, dann wird das Gitter gepunktet. Falls man eine durchgezogene Linie wünscht, lässt man diesen Parameter weg.
- subgriddots Wenn man das Gitter mit subgriddiv weiter unterteilt, kann man mit subgriddots auch die Unterteilung gepunktet zeichnen.
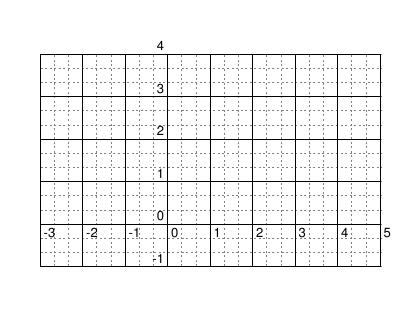
Hier ein Beispiel:
\documentclass{article}
\usepackage{pst-plot}
\begin{document}
\begin{center}
\begin{pspicture}(-3,-1)(5,4)
\psgrid[gridwidth=0.1pt,gridlabels=9pt,subgriddiv=3,subgriddots=4](0,0)(-3,-1)(5,4)
\end{pspicture}
\end{center}
\end{document}
Die Plottfunktion
Die 2-D-Plottfunktion hat folgendes Aussehen:
\psplot[Parameter]{untere Grenze}{obere Grenze}{Funktion}
Interessante Parameter sind:
- plotstyle=line / curve / dots/... Der Defaultwert ist line. Diese Einstellung ist OK.
- plotpoints=Anzahl Die Anzahl ist hier auf 50 eingestellt. Das reicht auch meistens. Es wird aber in der Literatur ein Wert von 200 empfohlen.
- linecolor=red / green / cyan /.... Falls man mehrere Funktionen in einer Grafik plotten möchte, kann man sie unterschiedlich färben. Die Defaulteinstellung ist black.
- linestyle=solid / dotted / dashed Die Defaulteinstellung ist solid. Das ergibt eine durchgezogene Linie.
Die Angabe der Funktion ist etwas kompliziert. Man muß die Regeln der Umgekehrt Polnischen Notation UPN anwenden. Wenn man 2 Zahlen addieren möchte, rechnet man nicht a+b sondern a b add. Es werden also erst die Argumente angegeben, dann die Rechenoperation. Hier ein paar der wichtigsten:
- Addition: a b add liefert a+b
- Subtraktion: a b sub liefert a-b
- Multiplikation: a b mul liefert a*b
- Division: a b div liefert a/b
- Quadratwurzel: a sqrt liefert die Quadratwurzel von a
- Sinus: a sin liefert den Sinus von a. Das Argument wird in Grad (0-360) angegeben.
- Natürlicher Logarithmus: a ln liefert den natürlichen Logarithmus
- Potenz: a b exp liefert a^b
Es gibt noch mehr. Eine wichtige Operation ist noch folgende:
- Duplizieren: a dup liefert a a. a^2 berechnet man also so: a dup mul, das ist das gleiche wie a a mul.
Beispiele
Die Funktion f(x)= x^2
Das erste klassische Beispiel ist die Funktion f(x)=x^2.
\documentclass{article}
\usepackage{pst-plot}
\begin{document}
\begin{center}
\begin{pspicture}[](-5,-1)(5,9)
\psclip{\psframe(-5,-1)(5,9) }
% \psgrid[subgriddiv=1, gridlabels=0pt, griddots=5]
\psaxes[]{->}(0,0)(-4,0)(4,9)
\psplot[linecolor=red]{-3}{3}{x x mul}
\endpsclip
\end{pspicture}
\end{center}
\end{document}
Die Sinusfunktion
Das Argument der von PSTricks bereitgestellten Sinusfunktion muß in Grad angegeben werden. Das heißt:
- sin(90) = 1
- sin(180) = 0
- sin(270) = -1
- sin(360) = 0
Das lässt sich jedoch schlecht plotten. Wir machen es uns einfach, und plotten statt sin(x) einfach sin(180*x).
\documentclass{article}
\usepackage{pst-plot}
\usepackage[left=1cm, right=1cm]{geometry}
\begin{document}
\begin{center}
\scalebox{3}{
\begin{pspicture}(-0,-1)(4,1)
\psgrid[gridwidth=0.1pt, gridlabels=0pt,subgriddiv=1]
\psaxes[linewidth=0.5pt,labels=none, ticks=none]{->}(0,0)(-0,-1)(4,1)
\psplot[plotstyle=curve]{-0}{4}{x 180 mul sin}
\rput(2.2, -0.41){$2\pi$}
\rput(4.2, -0.41){$4\pi$}
\end{pspicture}
} % Hier endet die scalebox
\end{center}
\end{document}
3-D-Plotts
Die 3-D-Plottfunktion
Die 3-D-Plottfunktion hat folgende Gestalt:
\psplotThreeD[ Alpha=45, Beta=30,
hiddenLine=false,%
plotstyle=curve,%
drawStyle=xLines,%
yPlotpoints=80, xPlotpoints=80,%
linewidth=0.1pt]%
(xunten,xoben)(yunten,yoben){Die Funktion}
Beschreibung der Parameter:
- Alpha: Eine Erhöhung von Alpha dreht das Bild horizontal gegen den Uhrzeigersinn. Die Defaulteinstellung ist 45.
- Beta: Eine Erhöhung von Beta kippt das Bild nach vorn. Die Defaulteinstellung ist 30.
- hiddenLine: Mögliche Parameter sind true/false. Die Wirkung ist schwer beschreiblich. Einfach ausprobieren! Die Defaulteinstellung ist false.
- plotstyle: Mögliche Parameter: none / curve / line / dots /... Die besten Ergebnisse erhält man mit dem Parameter curve. Auch dots ist interessant. Hinweis: Die Defaulteinstellung ist none! Es wird also per Default keine Kurve gezeichnet.
- drawStyle: Mögliche Parameter sind xLines / yLines / xyLines. Also Kurven über die x-, y- oder beide Achsen. Die Defaulteinstellung ist xLines.
- yPlotpoints: Defaulteinstellung ist 25. Das ist wohl zuwenig.
- xPlotpoints: Defaulteinstellung ist 25.
- linewidth: Die Defaulteinstellung ist etwas zu dick! Ich habe sie hier etwas dünner (0.1pt) eingestellt. Das ist aber Geschmacksache.
Hinweis: Die Parameter Alpha und Beta muß man nicht in der Plottfunktion angeben. Man könnte sie auch im Befehl \psset angeben:
\psset{Alpha=45, Beta=30}
Dies hätte den Vorteil, das die Parameter auch für ein eventuell angegebenes Koordinatensystem gelten. Im folgenden Beispiel habe ich das so gemacht.
Beispiele
Die Sinusfunktion in der Ebene
Wir zeichnen mitten in eine Ebene den Ursprung. Und von dort breiten sich Sinusschwingungen in alle Richtungen aus. Die Funktion lautet:
f(x,y) = sin(sqrt(x^2+y^2)
\documentclass{article}
\usepackage{pst-3dplot}
\begin{document}
\begin{center}
\begin{pspicture}(-3,3)(3,8)
\psset{Alpha=65,Beta=70,unit=2.0cm}
\psplotThreeD[ plotstyle=curve,%
drawStyle=xLines,%
yPlotpoints=80,xPlotpoints=80,%
linewidth=0.1pt]%
(-3,3)(-3,3){x 180 mul dup mul y 180 mul dup mul add sqrt sin}
\end{pspicture}
\end{center}
\end{document}
Zum Vergleich werden wir dieses Beispiel auch einmal mit Maxima plotten. Wir starten Maxima und geben folgenden Code ein:
plot3d(sin(sqrt(x^2+y^2)),[x,-10,10],[y,-10,10],[grid,70,70], [plot_format, openmath]);
| LaTeX: (1.) Einleitung - (2.) Schnellkurs - (3.) Teil 1 - Grundlagen - (4.) Teil 2 - Grundlagen - (5.) Fortgeschrittene - (6.) Literaturverzeichnisse - (7.) Zeichen und Symbole - (8.) LaTeX Distributionen - (9.) LaTeX Links |